# goFilter
**Repository Path**: luozh111/go-filter
## Basic Information
- **Project Name**: goFilter
- **Description**: 多区间查找问题
- **Primary Language**: Unknown
- **License**: Not specified
- **Default Branch**: master
- **Homepage**: None
- **GVP Project**: No
## Statistics
- **Stars**: 0
- **Forks**: 1
- **Created**: 2022-04-17
- **Last Updated**: 2024-05-26
## Categories & Tags
**Categories**: Uncategorized
**Tags**: None
## README
## 问题背景
最近遇到一个需求,场景大概如下。
给定若干个id,每个id有一个若干个覆盖区间(这些区间可能相互重复)。
每次查询过来,给定一个key,问该key是否命中这若干id中的至少一个,并求命中的所有id。key命中id,当且仅当这个key落在了这个id里边的其中一个区间内。
这个问题中,读取配置,重新加载的频率较低,查询的频率较高。关注的是查询速度。
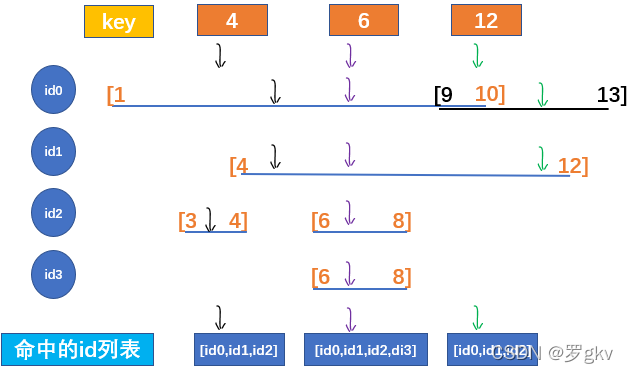
举个例子。有如下几个id。
```cpp
{
"0" : [[1, 10], [9, 13]],
"1" : [[4, 12]],
"2" : [[3, 4], [6, 8]],
"3" : [[6,8]]
}
```
- 如果key取5,那么它命中了id 0,1;
- 如果key取8,那么它命中了id 0,1,2,3;
- 如果key取13,那么它命中id 0。
- 如果key取14,则它没有命中id。
## 声明
n=id个数,m=每个id的平均区间个数。
以下的例子讲解均基于以下配置
```cpp
{
"0" : [[1, 10], [9, 13]],
"1" : [[4, 12]],
"2" : [[3, 4], [6, 8]],
"3" : [[6,8]]
}
```
## 暴力解法
### 存储
- 存储每个id对应的区间列表。
### 查询
遍历每个id,对于当前id,看它是否存在区间,包含 Key,从而判断 Key是否命中当前id。
### 查询时间复杂度
O(n*m)
## 二分优化
### 存储
- 整合所有id的区间,将区间的左下标、右下标分别存储在有序下标列表中。
- 对左下标列表和右下标列表,分别维护包含key的id列表。
- 对于左边界下标列表,维护包含key,且区间右边界大于key的id列表。
- 对于右边界下标列表,维护包含key,且区间左边界小于key的id列表。

### 查询
对于 Key,二分查找左区间列表中<= Key最近的lKey,以及右区间列表中>= Key最近的rKey。
1、如果左区间或右区间列表刚好存在 Key,则直接返回包含 Key的id列表。
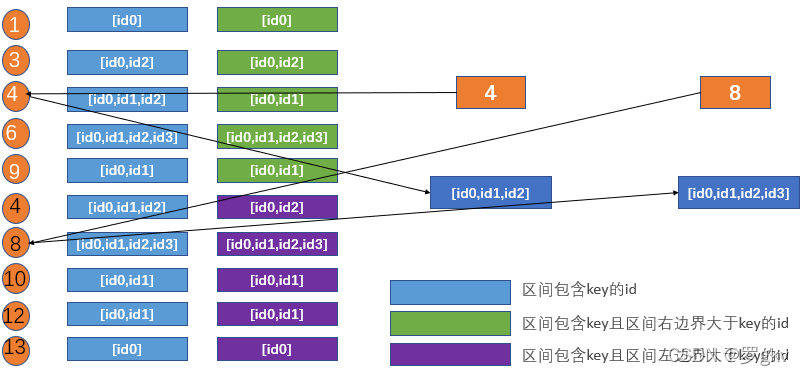
2、如果lKey不存在或rKey不存在,则无解
3、如果lKey和rKey同时存在,且 Key不在区间里边中,则取同时包含lKey, rKkey的id列表
证明:如果 Key取5,那么此时lKey为4,rKey为8。我们取lKey的绿色区间和rKey的紫色区间的交集,{[1,10],[4,12]},对应的id为id0,id1
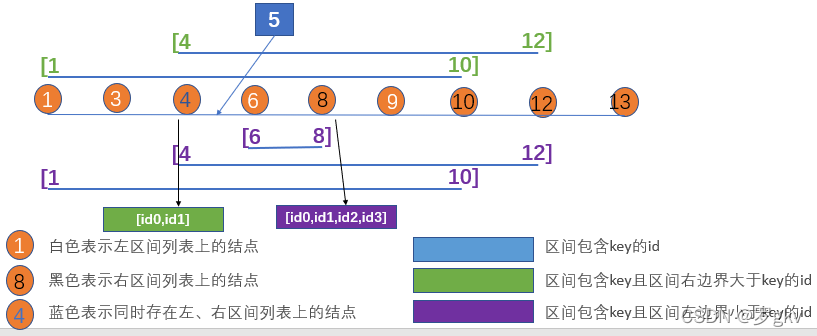
可以发现,同时包含lKey 4, rKey 8的区间,也一定包含 Key 5。
### 查询时间复杂度
O(log(n+m)+n+m)
## 二分再优化
### 存储
- 整合所有id的区间,将区间的下标存储在有序下标列表中。
- 对每个下标,维护包含key的id列表。
- 对于下标,维护包含key、及其相邻key的id列表。
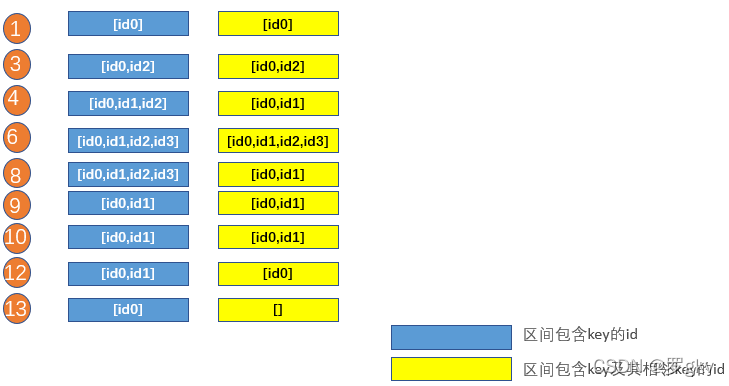
### 查询
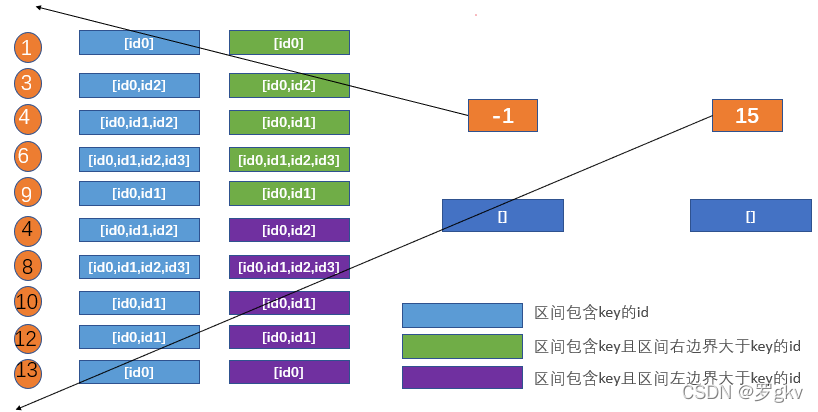
对于 Key,二分查找区间列表中<= Key最近的lKey。
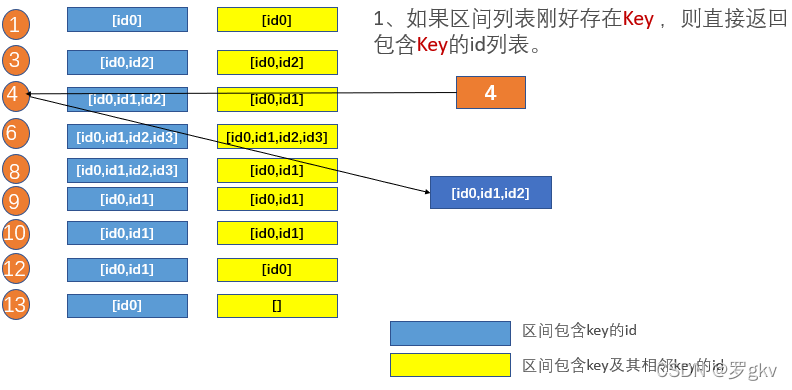
1、如果区间列表刚好存在 Key ,则直接返回包含 Key的id列表。
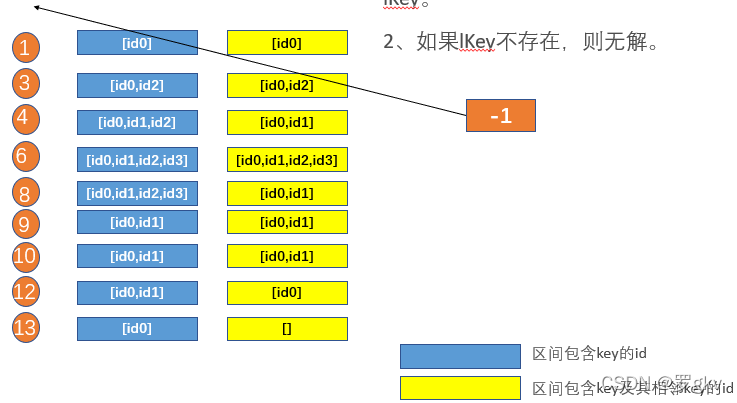
2、如果lKey不存在,则无解。
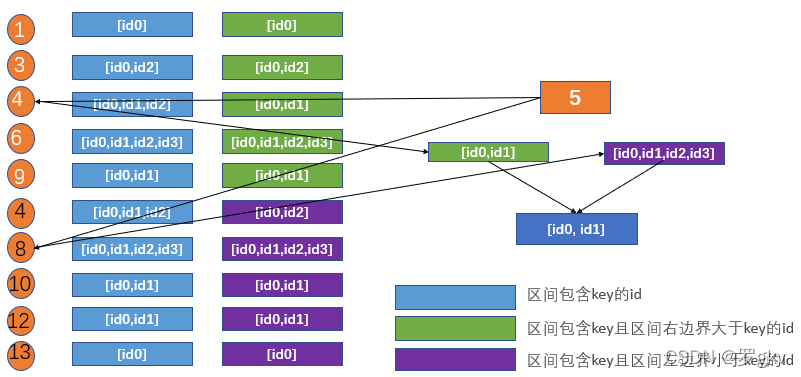
3、如果lKey存在且lKey不等于 Key ,则返回包含lKey及其相邻key的区间,所对应的id列表(黄色部分)。
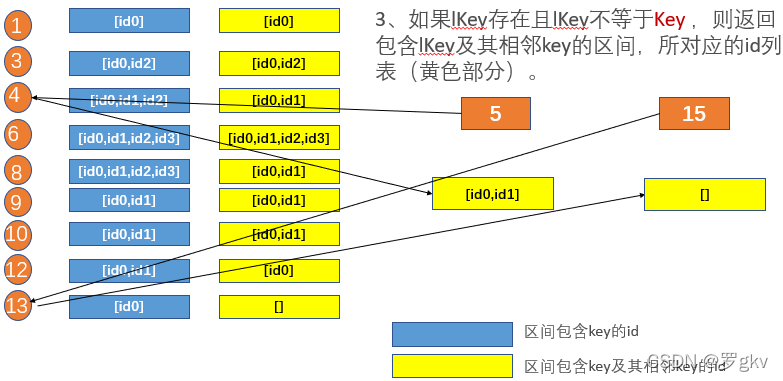
证明:如果 Key取5,那么此时lKey为4。我们取lKey的黄色区间{[1,10],[4,12]},对应的id为id0,id1
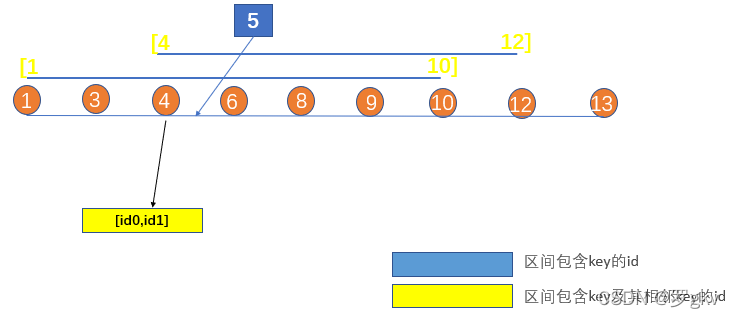
可以发现,同时包含lKey 4, 及其相邻key 6的区间,也一定包含 Key 5。
### 查询时间复杂度
时间复杂度O(log_{n+m})
[博客原文](https://blog.csdn.net/weixin_43918473/article/details/124088798)