# jqfactor_analyzer
**Repository Path**: yangzijing/jqfactor_analyzer
## Basic Information
- **Project Name**: jqfactor_analyzer
- **Description**: No description available
- **Primary Language**: Unknown
- **License**: MIT
- **Default Branch**: master
- **Homepage**: None
- **GVP Project**: No
## Statistics
- **Stars**: 0
- **Forks**: 0
- **Created**: 2025-06-08
- **Last Updated**: 2025-06-08
## Categories & Tags
**Categories**: Uncategorized
**Tags**: None
## README
# jqfactor_analyzer
jqfactor_analyzer 是提供给用户配合 jqdatasdk 进行归因分析,因子数据缓存及单因子分析的开源工具。
### 安装
```pip install jqfactor_analyzer```
### 升级
```pip install -U jqfactor_analyzer```
### 具体使用方法
**详细用法请查看[API文档](https://github.com/JoinQuant/jqfactor_analyzer/blob/master/docs/API%E6%96%87%E6%A1%A3.md)**
## 归因分析使用示例
### 风格模型的基本概念
归因分析旨在通过对历史投资组合的收益进行分解,明确指出各个收益来源对组合的业绩贡献,能够更好地理解组合的表现是否符合预期,以及是否存在某一风格/行业暴露过高的风险。
多因子风险模型的基础理论认为,股票的收益是由一些共同的因子 (风格,行业和国家因子) 来驱动的,不能被这些因子解释的部分被称为股票的 “特异收益”, 而每只股票的特异收益之间是互不相关的。
(1) 风格因子,即影响股票收益的风格因素,如市值、成长、杠杆等。
(2) 行业因子,不同行业在不同时期可能优于或者差于其他行业,同一行业内的股票往往涨跌具有较强的关联性。
(3) 国家因子,表示股票市场整体涨落对投资组合的收益影响,对于任意投资组合,若他们投资的都是同一市场则其承担的国家因子和收益是相同的。
(4) 特异收益,即无法被多因子风险模型解释的部分,也就是影响个股收益的特殊因素,如公司经营能力、决策等。
根据上述多因子风险模型,股票的收益可以表达为 :
$$
R_i = \underbrace{1 \cdot f_c} _{\text{国家因子收益}} + \underbrace{\sum _{j=1}^{S} f _j^{style} \cdot X _{ij}^{style}} _{\text{风格因子收益}} + \underbrace{\sum _{j=1}^{I} f _j^{industry} \cdot X _{ij}^{industry}} _{\text{行业因子收益}} + \underbrace{u _i} _{\text{个股特异收益}}
$$
此公式可简化为:
$$
R_i = \underbrace{\sum_{j=1}^{K} f_j \cdot X_{ij}}_{\text{第 j 个因子 (含国家,风格和行业,总数为 K) 获得的收益}} + \underbrace{u_i} _{\text{个股特异收益}}
$$
其中:
- $R_i$ 是第 $i$ 只股票的收益
- $f_c$ 是国家因子的回报率
- $S$ 和 $I$ 分别是风格和行业因子的数量
- $f_j^{style}$ 是第 $j$ 个风格因子的回报率, $f_j^{industry}$ 是第 $j$ 个行业因子的回报率
- $X_{ij}^{style}$ 是第 $i$ 只股票在第 $j$ 个风格因子上的暴露, $X_{ij}^{industry}$ 是第 $i$ 只股票在第 $j$ 个行业因子上的暴露,因子暴露又称因子载荷/因子值 (通过`jqdatasdk.get_factor_values`可获取风格因子暴露及行业暴露哑变量)
- $u_i$ 是残差项,表示无法通过模型解释的部分 (即特异收益率)
根据上述公式,对市场上的股票 (一般采用中证全指作为股票池) 使用对数市值加权在横截面上进行加权最小二乘回归,可得到 :
- $f_j$ : 风格/行业因子和国家因子的回报率 , 通过 `jqdatasdk.get_factor_style_returns` 获取
- $u_i$ : 回归残差 (无法被模型解释的部分,即特异收益率), 通过 `jqdatasdk.get_factor_specific_returns` 获取
### 使用上述已提供的数据进行归因分析 :
现已知你的投资组合 P 由权重 $w_n$ 构成,则投资组合第 j 个因子的暴露可表示为 :
$$
X^P_j = \sum_{i=1}^{n} w_i X_{ij}
$$
- $X^P_j$ 可通过 `jqfactor_analyzer.AttributionAnalysis().exposure_portfolio` 获取
投资组合在第 j 个因子上获取到的收益率可以表示为 :
$$
R^P_j = X^P_j \cdot f_j
$$
- $R^P_j$ 可通过 `jqfactor_analyzer.AttributionAnalysis().attr_daily_return` 获取
所以投资组合的收益率也可以被表示为 :
$$
R_P = \sum_{j=1}^{k} R^p_j \cdot f_j + \sum_{i-1}^{n} w_i u_i
$$
即理论上 $\sum_n w_n u_n$ 就是投资组合的特异收益 (alpha) $R_s$ (您也可以直接获取个股特异收益率与权重相乘直接进行计算),但现实中受到仓位,调仓时间,费用等其他因素的影响,此公式并非完全成立的,AttributionAnalysis 中是使用做差的方式来计算特异收益率,即:
$$
R_s = R_P - \sum_{j=1}^{k} R^p_j \cdot f_j
$$
### 以指数作为基准的归因分析
- jqdatasdk 已经根据指数权重计算好了指数的风格暴露 $X^B$,可通过`jqdatasdk.get_index_style_exposure` 获取
投资组合 P 相对于指数的第 j 个因子的暴露可表示为 :
$$
X^{P2B}_j = X^P_j - X^B_j
$$
- $X^{P2B}_j$ 可通过 `jqfactor_analyzer.AttributionAnalysis().get_exposure2bench(index_symbol)` 获取
投资组合在第 j 个因子上相对于指数获取到的收益率可以表示为 :
$$
R^{P2B}_j = R^P_j - R^B_j = X^P_j \cdot f_j - X^B_j \cdot f_j = f_j \cdot X^{P2B}_j
$$
在 AttributionAnalysis 中,风格及行业因子部分,将指数的仓位和持仓的仓位进行了对齐;同时考虑了现金产生的收益 (国家因子在仓位对齐后不会产生暴露收益,现金收益为 0,现金相对于指数的收益即为:(-1) × 剩余仓位 × 指数收益)
所以投资组合相对于指数的收益可以被表示为:
$$
R_{P2B} = \sum_{j=1}^{k} R^{P2B}_j + R^{P2B}_s + 现金相对于指数的收益
$$
- $R_{P2B}$ 等可通过 `jqfactor_analyzer.AttributionAnalysis().get_attr_daily_returns2bench(index_symbol)` 获取
### 累积收益的处理
上述 `attr_daily_return` 和 `get_attr_daily_returns2bench(index_symbol)` 获取到的均为单日收益率,在计算累积收益时需要考虑复利影响。
$$
N_t = \prod_{t=1}^{n} (R^p_t+1)
$$
$$
Rcum^p_{jt} = N_{t-1} \cdot R^P_{jt}
$$
其中 :
- $N_t$ 为投资组合在第 t 天盘后的净值
- $R^p_t$ 为投资组合在第 t 天的日度收益率
- $Rcum^p_{jt}$ 为投资组合 p 的第 j 个因子在 t 日的累积收益
- $R^P_{jt}$ 为投资组合 p 的第 j 个因子在 t 日的日收益率
- $N_t, Rcum^p_{jt}$ 均可通过 `jqfactor_analyzer.AttributionAnalysis().attr_returns` 获取
- 相对于基准的累积收益算法类似, 可通过 `jqfactor_analyzer.AttributionAnalysis().get_attr_returns2bench` 获取
### 导入模块并登陆 jqdatasdk
```python
import jqdatasdk
import jqfactor_analyzer as ja
# 获取 jqdatasdk 授权,输入用户名、密码,申请地址:https://www.joinquant.com/default/index/sdk
# 聚宽官网,使用方法参见:https://www.joinquant.com/help/api/doc?name=JQDatadoc
jqdatasdk.auth("账号", "密码")
```
### 处理权重信息
此处使用的是 jqfactor_analyzer 提供的示例文件
数据格式要求 :
- 权重数据, 一个 dataframe, index 为日期, columns 为标的代码 (可使用 jqdatasdk.normalize_code 转为支持的格式), values 为权重, 每日的权重和应该小于 1
- 组合的日度收益数据, 一个 series, index 为日期, values 为日收益率
```python
import os
import pandas as pd
weight_path = os.path.join(os.path.dirname(ja.__file__), 'sample_data', 'weight_info.csv')
weight_infos = pd.read_csv(weight_path, index_col=0)
daily_return = weight_infos.pop("return")
```
```python
weight_infos.head(5)
```
|
000006.XSHE |
000008.XSHE |
000009.XSHE |
000012.XSHE |
000021.XSHE |
000025.XSHE |
000027.XSHE |
000028.XSHE |
000031.XSHE |
000032.XSHE |
... |
603883.XSHG |
603885.XSHG |
603888.XSHG |
603893.XSHG |
603927.XSHG |
603939.XSHG |
603979.XSHG |
603983.XSHG |
605117.XSHG |
605358.XSHG |
| 2020-01-02 |
0.000873 |
0.001244 |
0.002934 |
0.001219 |
0.001614 |
0.000433 |
0.001274 |
0.001181 |
0.001471 |
NaN |
... |
0.001294 |
0.001536 |
0.000781 |
NaN |
NaN |
0.001896 |
NaN |
0.000482 |
NaN |
NaN |
| 2020-01-03 |
0.000897 |
0.001247 |
0.002679 |
0.001203 |
0.001708 |
0.000432 |
0.001293 |
0.001195 |
0.001463 |
NaN |
... |
0.001298 |
0.001505 |
0.000824 |
NaN |
NaN |
0.001912 |
NaN |
0.000466 |
NaN |
NaN |
| 2020-01-06 |
0.000879 |
0.001216 |
0.002926 |
0.001225 |
0.001613 |
0.000434 |
0.001278 |
0.001228 |
0.001429 |
NaN |
... |
0.001238 |
0.001534 |
0.000767 |
NaN |
NaN |
0.001962 |
NaN |
0.000488 |
NaN |
NaN |
| 2020-01-07 |
0.000883 |
0.001241 |
0.002591 |
0.001220 |
0.001536 |
0.000439 |
0.001294 |
0.001195 |
0.001488 |
NaN |
... |
0.001267 |
0.001575 |
0.000764 |
NaN |
NaN |
0.001959 |
NaN |
0.000468 |
NaN |
NaN |
| 2020-01-08 |
0.000877 |
0.001231 |
0.002758 |
0.001205 |
0.001528 |
0.000429 |
0.001270 |
0.001208 |
0.001448 |
NaN |
... |
0.001277 |
0.001554 |
0.000749 |
NaN |
NaN |
0.001987 |
NaN |
0.000474 |
NaN |
NaN |
5 rows × 818 columns
```python
weight_infos.sum(axis=1).head(5)
```
2020-01-02 0.752196
2020-01-03 0.750206
2020-01-06 0.752375
2020-01-07 0.752054
2020-01-08 0.748039
dtype: float64
### 进行归因分析
**具体用法请查看[API文档](https://github.com/JoinQuant/jqfactor_analyzer/blob/master/docs/API%E6%96%87%E6%A1%A3.md), 此处仅作示例**
```python
An = ja.AttributionAnalysis(weight_infos, daily_return, style_type='style', industry='sw_l1', use_cn=True, show_data_progress=True)
```
check/save factor cache : 100%|██████████| 54/54 [00:02<00:00, 25.75it/s]
calc_style_exposure : 100%|██████████| 1087/1087 [00:27<00:00, 39.52it/s]
calc_industry_exposure : 100%|██████████| 1087/1087 [00:19<00:00, 56.53it/s]
```python
An.exposure_portfolio.head(5) #查看暴露
```
|
size |
beta |
momentum |
residual_volatility |
non_linear_size |
book_to_price_ratio |
liquidity |
earnings_yield |
growth |
leverage |
... |
801050 |
801040 |
801780 |
801970 |
801120 |
801790 |
801760 |
801890 |
801960 |
country |
| 2020-01-02 |
-0.487816 |
0.468947 |
-0.048262 |
0.104597 |
0.976877 |
-0.112042 |
0.278131 |
-0.311944 |
-0.000541 |
-0.356787 |
... |
0.030234 |
0.023728 |
0.010499 |
NaN |
0.017049 |
0.032292 |
0.042405 |
0.027871 |
NaN |
0.752196 |
| 2020-01-03 |
-0.485128 |
0.461138 |
-0.044422 |
0.104270 |
0.970710 |
-0.110196 |
0.271739 |
-0.314469 |
-0.002360 |
-0.354623 |
... |
0.030574 |
0.023712 |
0.010610 |
NaN |
0.017071 |
0.033261 |
0.041491 |
0.027631 |
NaN |
0.750206 |
| 2020-01-06 |
-0.477658 |
0.464642 |
-0.034905 |
0.116226 |
0.958563 |
-0.118501 |
0.277993 |
-0.320429 |
-0.001766 |
-0.352186 |
... |
0.030807 |
0.023681 |
0.010619 |
NaN |
0.016953 |
0.033203 |
0.042406 |
0.027906 |
NaN |
0.752375 |
| 2020-01-07 |
-0.474913 |
0.456438 |
-0.030596 |
0.118867 |
0.953152 |
-0.117436 |
0.274219 |
-0.315071 |
-0.000874 |
-0.350100 |
... |
0.030140 |
0.024215 |
0.010716 |
NaN |
0.017240 |
0.033022 |
0.042867 |
0.027853 |
NaN |
0.752054 |
| 2020-01-08 |
-0.474413 |
0.452745 |
-0.026417 |
0.123923 |
0.951369 |
-0.115294 |
0.271193 |
-0.305295 |
-0.000920 |
-0.345431 |
... |
0.030176 |
0.023694 |
0.010671 |
NaN |
0.017303 |
0.032777 |
0.040977 |
0.027820 |
NaN |
0.748039 |
5 rows × 43 columns
```python
An.attr_daily_returns.head(5) #查看日度收益拆解
```
|
size |
beta |
momentum |
residual_volatility |
non_linear_size |
book_to_price_ratio |
liquidity |
earnings_yield |
growth |
leverage |
... |
801970 |
801120 |
801790 |
801760 |
801890 |
801960 |
country |
common_return |
specific_return |
total_return |
| 2020-01-02 |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
... |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
0.000000 |
NaN |
NaN |
| 2020-01-03 |
0.000241 |
-0.000144 |
0.000130 |
0.000090 |
0.000955 |
-0.000039 |
-0.000045 |
0.000174 |
7.907650e-08 |
0.000148 |
... |
NaN |
-0.000168 |
-0.000019 |
0.000500 |
-0.000050 |
NaN |
0.000860 |
0.003030 |
-0.001083 |
0.001948 |
| 2020-01-06 |
-0.000014 |
0.000151 |
0.000119 |
0.000199 |
0.002035 |
-0.000017 |
0.000025 |
0.000573 |
-1.457480e-07 |
0.000160 |
... |
NaN |
-0.000178 |
-0.000145 |
0.000286 |
0.000015 |
NaN |
0.000949 |
0.004990 |
0.002358 |
0.007348 |
| 2020-01-07 |
0.000176 |
0.001208 |
0.000002 |
0.000236 |
0.001533 |
0.000012 |
-0.000213 |
-0.000627 |
8.726552e-07 |
0.000250 |
... |
NaN |
0.000077 |
-0.000003 |
0.000834 |
-0.000008 |
NaN |
0.006875 |
0.009541 |
-0.000621 |
0.008920 |
| 2020-01-08 |
-0.000190 |
-0.001919 |
-0.000007 |
0.000019 |
0.000199 |
0.000027 |
-0.000134 |
0.000400 |
-8.393073e-09 |
-0.000140 |
... |
NaN |
0.000038 |
-0.000384 |
-0.000414 |
0.000104 |
NaN |
-0.009655 |
-0.010019 |
-0.000516 |
-0.010535 |
5 rows × 46 columns
```python
An.attr_returns.head(5) #查看累积收益
```
|
size |
beta |
momentum |
residual_volatility |
non_linear_size |
book_to_price_ratio |
liquidity |
earnings_yield |
growth |
leverage |
... |
801970 |
801120 |
801790 |
801760 |
801890 |
801960 |
country |
common_return |
specific_return |
total_return |
| 2020-01-02 |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
... |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
| 2020-01-03 |
0.000241 |
-0.000144 |
0.000130 |
0.000090 |
0.000955 |
-0.000039 |
-0.000045 |
0.000174 |
7.907650e-08 |
0.000148 |
... |
NaN |
-0.000168 |
-0.000019 |
0.000500 |
-0.000050 |
NaN |
0.000860 |
0.003030 |
-0.001083 |
0.001948 |
| 2020-01-06 |
0.000227 |
0.000007 |
0.000249 |
0.000290 |
0.002994 |
-0.000056 |
-0.000020 |
0.000748 |
-6.695534e-08 |
0.000308 |
... |
NaN |
-0.000346 |
-0.000164 |
0.000787 |
-0.000035 |
NaN |
0.001812 |
0.008030 |
0.001280 |
0.009310 |
| 2020-01-07 |
0.000405 |
0.001226 |
0.000252 |
0.000528 |
0.004541 |
-0.000044 |
-0.000234 |
0.000115 |
8.138242e-07 |
0.000560 |
... |
NaN |
-0.000268 |
-0.000168 |
0.001629 |
-0.000043 |
NaN |
0.008750 |
0.017660 |
0.000653 |
0.018313 |
| 2020-01-08 |
0.000212 |
-0.000728 |
0.000245 |
0.000547 |
0.004744 |
-0.000016 |
-0.000371 |
0.000522 |
8.052775e-07 |
0.000418 |
... |
NaN |
-0.000229 |
-0.000559 |
0.001207 |
0.000064 |
NaN |
-0.001081 |
0.007457 |
0.000128 |
0.007585 |
5 rows × 46 columns
```python
An.get_attr_returns2bench('000905.XSHG').head(5) #查看相对指数的累积收益
```
|
size |
beta |
momentum |
residual_volatility |
non_linear_size |
book_to_price_ratio |
liquidity |
earnings_yield |
growth |
leverage |
... |
801970 |
801120 |
801790 |
801760 |
801890 |
801960 |
common_return |
cash |
specific_return |
total_return |
| 2020-01-02 |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
... |
NaN |
NaN |
NaN |
NaN |
NaN |
NaN |
0.000000 |
0.000000 |
0.000000 |
0.000000 |
| 2020-01-03 |
2.247752e-08 |
5.274612e-07 |
-1.010579e-06 |
-1.780933e-07 |
-5.018849e-09 |
-1.576053e-07 |
1.815168e-07 |
3.067299e-07 |
-8.676436e-08 |
3.843589e-07 |
... |
NaN |
-8.367921e-07 |
2.211999e-07 |
2.512287e-07 |
-2.031997e-07 |
NaN |
-0.000006 |
-0.000670 |
-0.000079 |
-0.000755 |
| 2020-01-06 |
3.139000e-09 |
-2.167887e-06 |
1.005890e-06 |
-9.837778e-06 |
1.803920e-06 |
3.592758e-07 |
-3.082887e-07 |
-4.489268e-06 |
-1.570012e-07 |
-7.565016e-07 |
... |
NaN |
-4.620739e-06 |
-2.607788e-06 |
-8.734669e-06 |
-1.166518e-07 |
NaN |
-0.000063 |
-0.003198 |
-0.000234 |
-0.003494 |
| 2020-01-07 |
-5.129552e-08 |
-2.485408e-05 |
9.140735e-07 |
-2.227106e-05 |
1.453669e-06 |
-5.066033e-08 |
4.500972e-06 |
4.348111e-06 |
1.794315e-07 |
-3.707358e-06 |
... |
NaN |
-1.876927e-06 |
-2.703177e-06 |
-3.476170e-05 |
-2.429496e-07 |
NaN |
-0.000095 |
-0.006224 |
-0.000283 |
-0.006603 |
| 2020-01-08 |
-1.236180e-07 |
4.020758e-05 |
1.082783e-06 |
-2.386474e-05 |
1.502709e-06 |
-1.806807e-06 |
1.001751e-05 |
-7.241071e-06 |
1.893800e-07 |
-1.425501e-06 |
... |
NaN |
2.019730e-07 |
-1.379156e-05 |
-1.232299e-05 |
1.799073e-06 |
NaN |
-0.000087 |
-0.002647 |
-0.000427 |
-0.003160 |
5 rows × 46 columns
```python
An.plot_exposure(factors='style',index_symbol=None,figsize=(15,7))
```
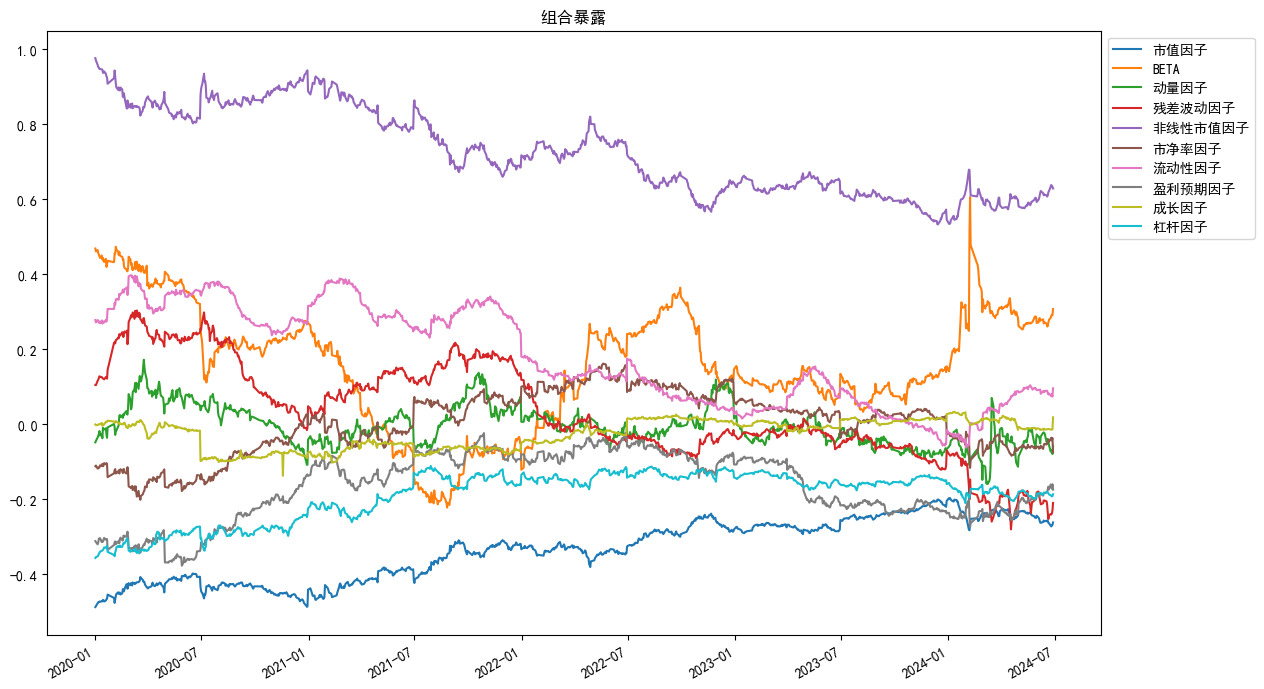
```python
An.plot_returns(factors='style',index_symbol=None,figsize=(15,7))
```
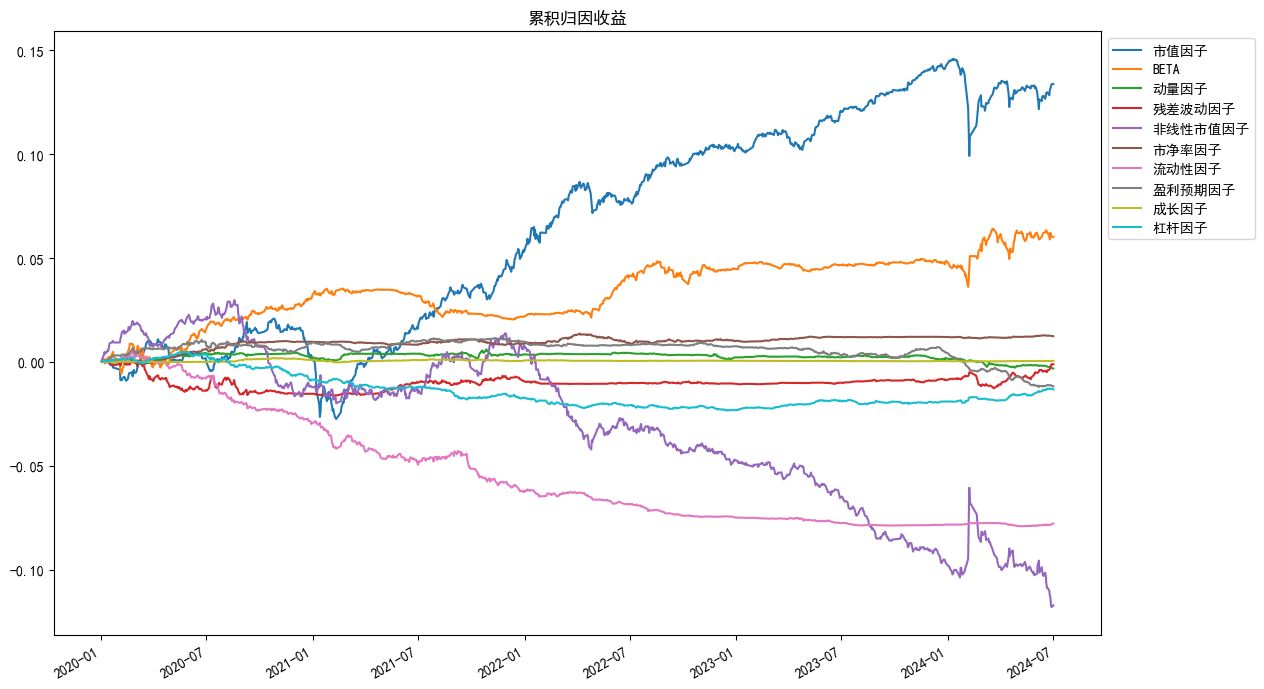
```python
An.plot_exposure_and_returns(factors='style',index_symbol=None,show_factor_perf=False,figsize=(12,6))
```
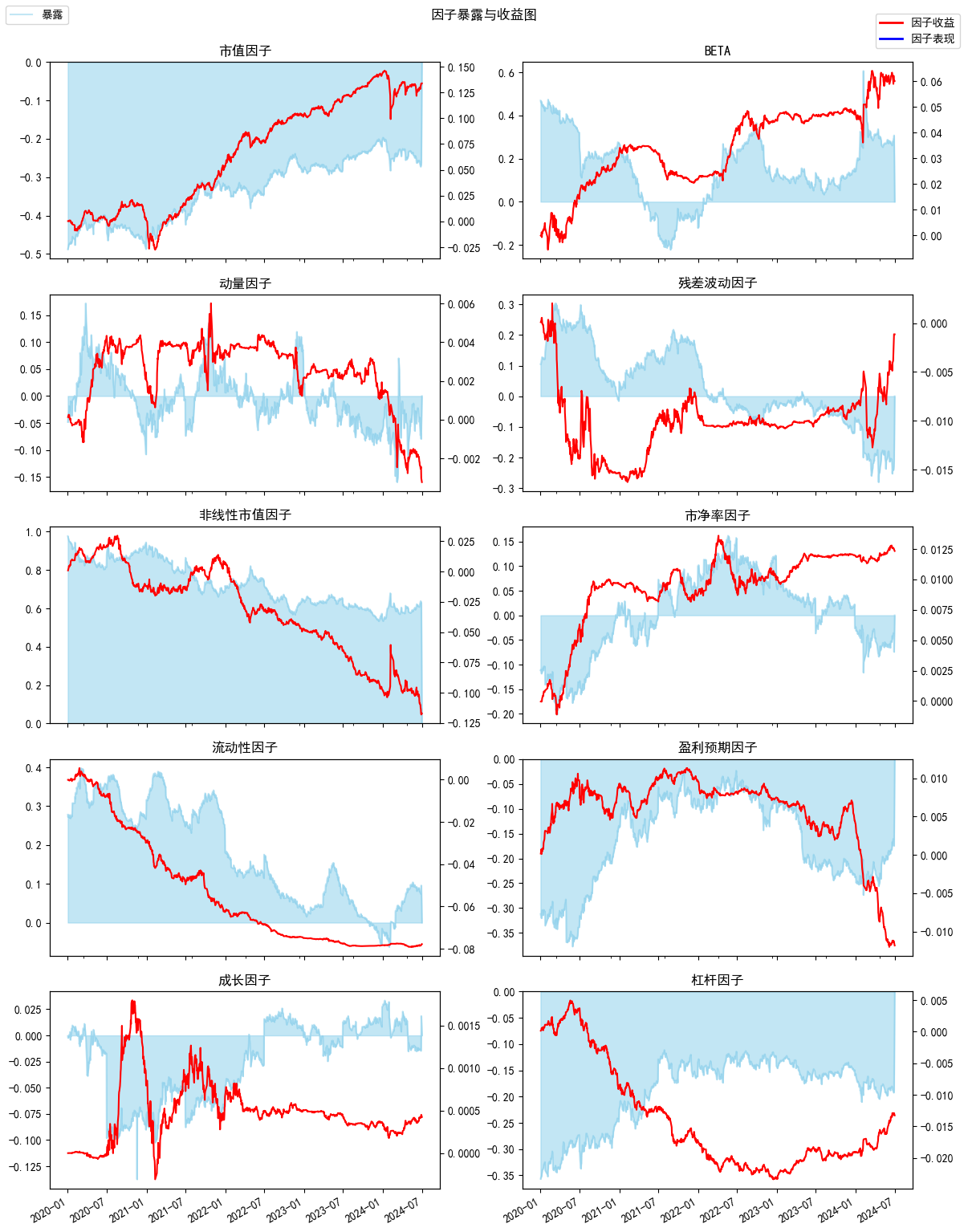
## 因子数据本地缓存使用示例
**具体用法请查看[API文档](https://github.com/JoinQuant/jqfactor_analyzer/blob/master/docs/API%E6%96%87%E6%A1%A3.md), 此处仅作示例**
### 设置缓存目录
```python
from jqfactor_analyzer.factor_cache import set_cache_dir,get_cache_dir
# my_path = 'E:\\jqfactor_cache'
# set_cache_dir(my_path) #设置缓存目录为my_path
print(get_cache_dir()) #输出缓存目录
```
C:\Users\wq\jqfactor_datacache\bundle
### 缓存/检查缓存和读取已缓存数据
```python
from jqfactor_analyzer.factor_cache import save_factor_values_by_group,get_factor_values_by_cache,get_factor_folder,get_cache_dir
# import jqdatasdk as jq
# jq.auth("账号",'密码') #登陆jqdatasdk来从服务端缓存数据
all_factors = jqdatasdk.get_all_factors()
factor_names = all_factors[all_factors.category=='growth'].factor.tolist() #将聚宽因子库中的成长类因子作为一组因子
group_name = 'growth_factors' #因子组名定义为'growth_factors'
start_date = '2021-01-01'
end_date = '2021-06-01'
# 检查/缓存因子数据
factor_path = save_factor_values_by_group(start_date,end_date,factor_names=factor_names,group_name=group_name,overwrite=False,show_progress=True)
# factor_path = os.path.join(get_cache_dir(), get_factor_folder(factor_names,group_name=group_name) #等同于save_factor_values_by_group返回的路径
```
check/save factor cache : 100%|██████████| 6/6 [00:01<00:00, 5.87it/s]
```python
# 循环获取缓存的因子数据,并拼接
trade_days = jqdatasdk.get_trade_days(start_date,end_date)
factor_values = {}
for date in trade_days:
factor_values[date] = get_factor_values_by_cache(date,codes=None,factor_names=factor_names,group_name=group_name, factor_path=factor_path)#这里实际只需要指定group_name,factor_names参数的其中一个,缓存时指定了group_name时,factor_names不生效
factor_values = pd.concat(factor_values)
factor_values.head(5)
```
|
|
financing_cash_growth_rate |
net_asset_growth_rate |
net_operate_cashflow_growth_rate |
net_profit_growth_rate |
np_parent_company_owners_growth_rate |
operating_revenue_growth_rate |
PEG |
total_asset_growth_rate |
total_profit_growth_rate |
|
code |
|
|
|
|
|
|
|
|
|
| 2021-01-04 |
000001.XSHE |
4.218607 |
0.245417 |
-3.438636 |
-0.036129 |
-0.036129 |
0.139493 |
NaN |
0.172409 |
-0.053686 |
| 000002.XSHE |
-1.059306 |
0.236022 |
0.266020 |
0.009771 |
0.064828 |
0.115457 |
1.229423 |
0.107217 |
-0.013790 |
| 000004.XSHE |
NaN |
11.430834 |
-0.019530 |
-3.350306 |
-3.551808 |
-0.328126 |
NaN |
10.912087 |
-3.888289 |
| 000005.XSHE |
-1.014341 |
0.052103 |
-2.331018 |
-0.480705 |
-0.461062 |
-0.700859 |
NaN |
-0.040798 |
-0.567470 |
| 000006.XSHE |
-0.978757 |
0.112236 |
-1.509728 |
0.083089 |
0.044869 |
0.170041 |
1.931730 |
-0.005611 |
0.113066 |
## 单因子分析使用示例
**具体用法请查看[API文档](https://github.com/JoinQuant/jqfactor_analyzer/blob/master/docs/API%E6%96%87%E6%A1%A3.md), 此处仅作示例**
### 示例:5日平均换手率因子分析
```python
# 载入函数库
import pandas as pd
import jqfactor_analyzer as ja
# 获取5日平均换手率因子2018-01-01到2018-12-31之间的数据(示例用从库中直接调取)
# 聚宽因子库数据获取方法在下方
from jqfactor_analyzer.sample import VOL5
factor_data = VOL5
# 对因子进行分析
far = ja.analyze_factor(
factor_data, # factor_data 为因子值的 pandas.DataFrame
quantiles=10,
periods=(1, 10),
industry='jq_l1',
weight_method='avg',
max_loss=0.1
)
# 获取整理后的因子的IC值
far.ic
```
check/save price cache : 100%|██████████| 13/13 [00:00<00:00, 25.60it/s]
load price info : 100%|██████████| 253/253 [00:06<00:00, 38.09it/s]
load industry info : 100%|██████████| 243/243 [00:00<00:00, 331.46it/s]
|
period_1 |
period_10 |
| date |
|
|
| 2018-01-02 |
0.141204 |
-0.058936 |
| 2018-01-03 |
0.082738 |
-0.176327 |
| 2018-01-04 |
-0.183788 |
-0.196901 |
| 2018-01-05 |
0.057023 |
-0.180102 |
| 2018-01-08 |
-0.025403 |
-0.187145 |
| ... |
... |
... |
| 2018-12-24 |
0.098161 |
-0.198127 |
| 2018-12-25 |
-0.269072 |
-0.166092 |
| 2018-12-26 |
-0.430034 |
-0.117108 |
| 2018-12-27 |
-0.107514 |
-0.040684 |
| 2018-12-28 |
-0.013224 |
0.039446 |
243 rows × 2 columns
```python
# 生成统计图表
far.create_full_tear_sheet(
demeaned=False, group_adjust=False, by_group=False,
turnover_periods=None, avgretplot=(5, 15), std_bar=False
)
```
分位数统计
|
min |
max |
mean |
std |
count |
count % |
| factor_quantile |
|
|
|
|
|
|
| 1 |
0.00000 |
0.30046 |
0.072019 |
0.056611 |
7293 |
10.054595 |
| 2 |
0.08846 |
0.49034 |
0.198844 |
0.066169 |
7266 |
10.017371 |
| 3 |
0.14954 |
0.65984 |
0.309961 |
0.089310 |
7219 |
9.952574 |
| 4 |
0.22594 |
0.80136 |
0.423978 |
0.111141 |
7248 |
9.992555 |
| 5 |
0.30904 |
0.99400 |
0.553684 |
0.133578 |
7280 |
10.036672 |
| 6 |
0.38860 |
1.23760 |
0.696531 |
0.166341 |
7211 |
9.941545 |
| 7 |
0.48394 |
1.56502 |
0.874488 |
0.204828 |
7240 |
9.981526 |
| 8 |
0.61900 |
2.09560 |
1.132261 |
0.265739 |
7226 |
9.962225 |
| 9 |
0.84984 |
3.30790 |
1.639863 |
0.436992 |
7261 |
10.010478 |
| 10 |
1.23172 |
40.47726 |
4.276270 |
3.640945 |
7290 |
10.050459 |
-------------------------
收益分析
|
period_1 |
period_10 |
| Ann. alpha |
-0.087 |
-0.060 |
| beta |
1.218 |
1.238 |
| Mean Period Wise Return Top Quantile (bps) |
-20.913 |
-18.530 |
| Mean Period Wise Return Bottom Quantile (bps) |
-6.156 |
-6.452 |
| Mean Period Wise Spread (bps) |
-14.757 |
-13.177 |
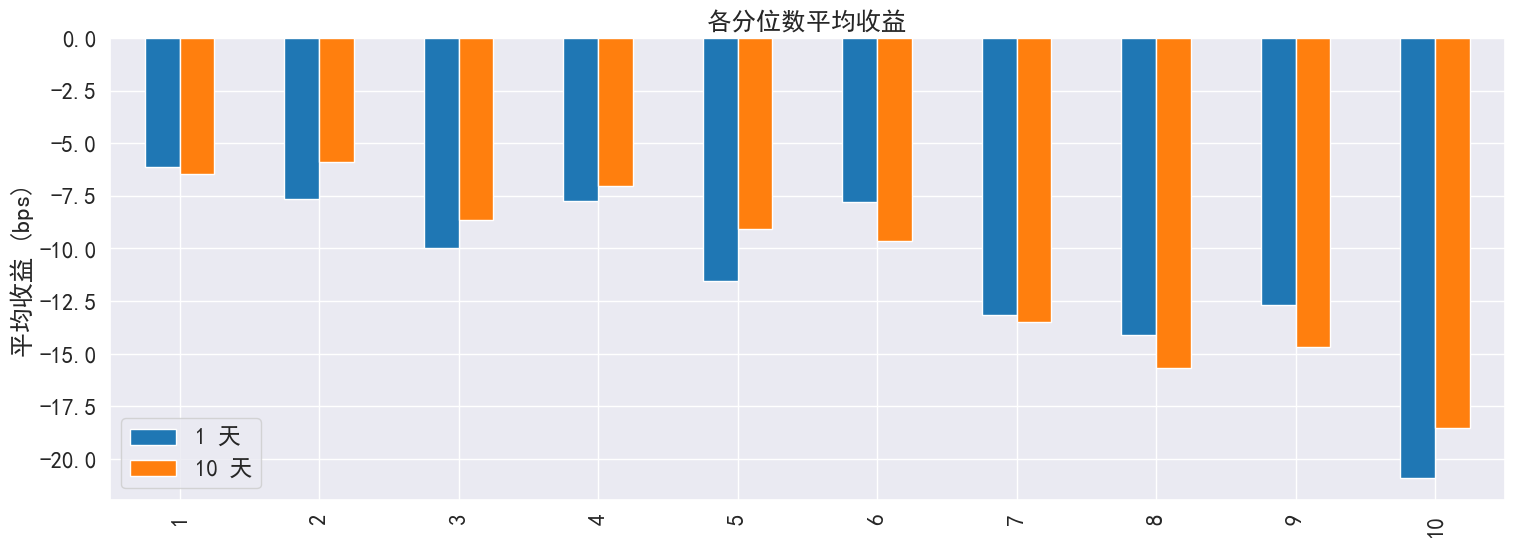
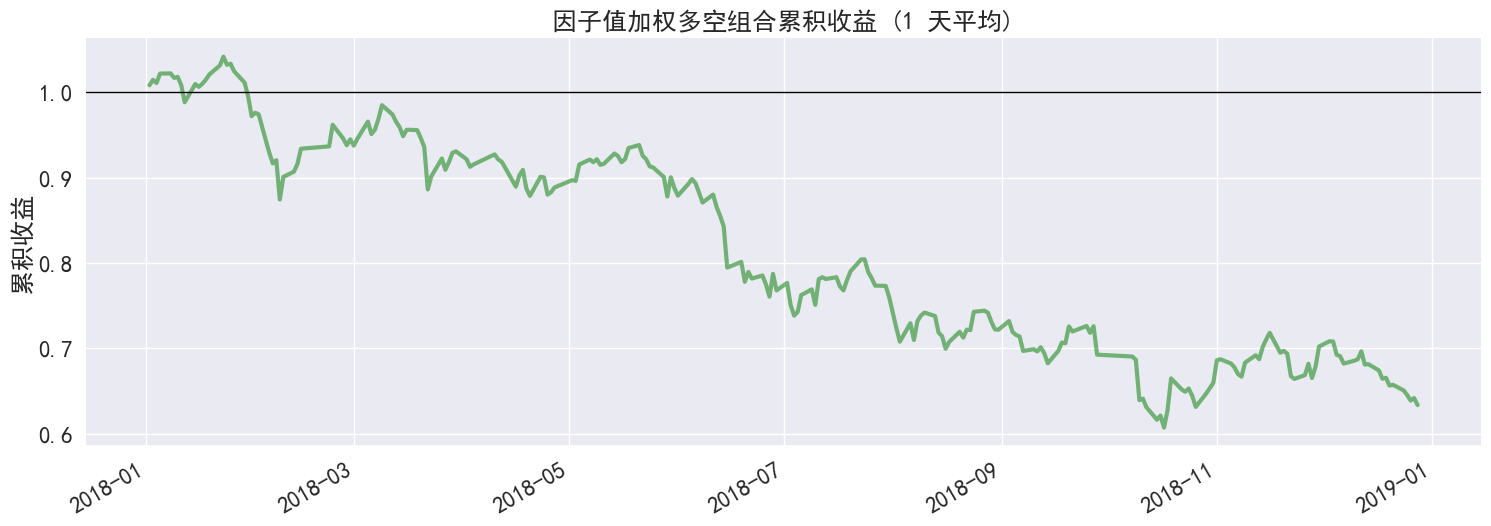
......(图片过多,此处内容演示已省略,请参考api说明使用)
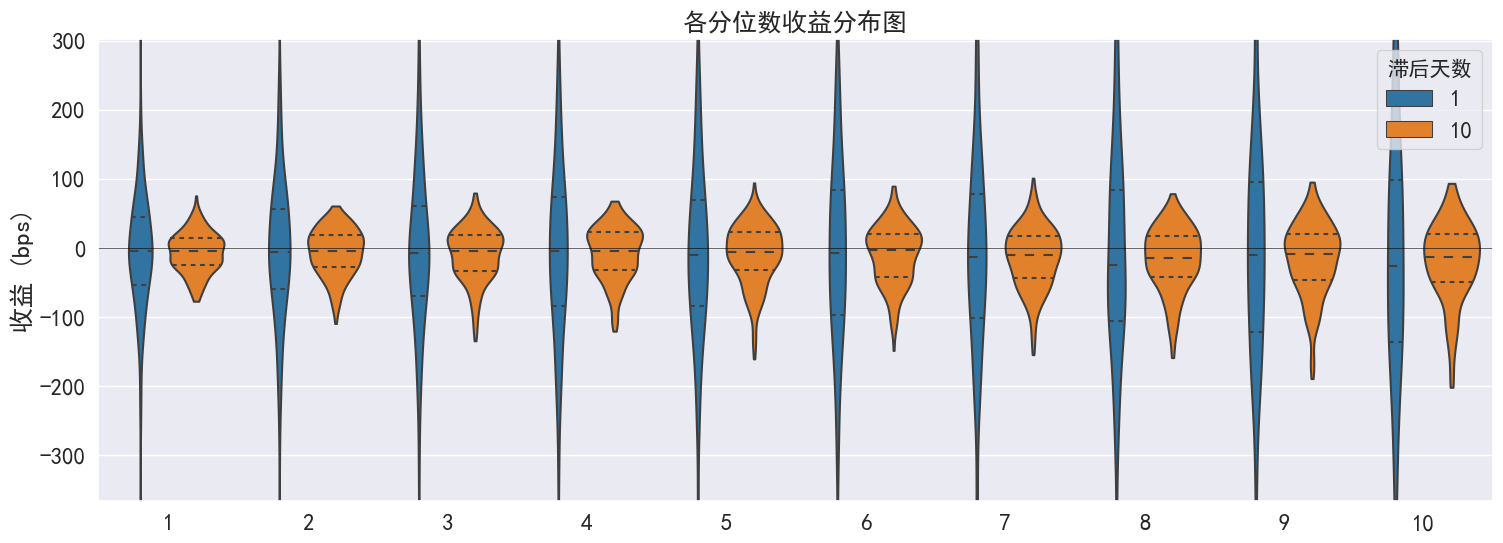
-------------------------
IC 分析
|
period_1 |
period_10 |
| IC Mean |
-0.030 |
-0.085 |
| IC Std. |
0.213 |
0.176 |
| IR |
-0.140 |
-0.487 |
| t-stat(IC) |
-2.180 |
-7.587 |
| p-value(IC) |
0.030 |
0.000 |
| IC Skew |
0.240 |
0.091 |
| IC Kurtosis |
-0.420 |
-0.485 |
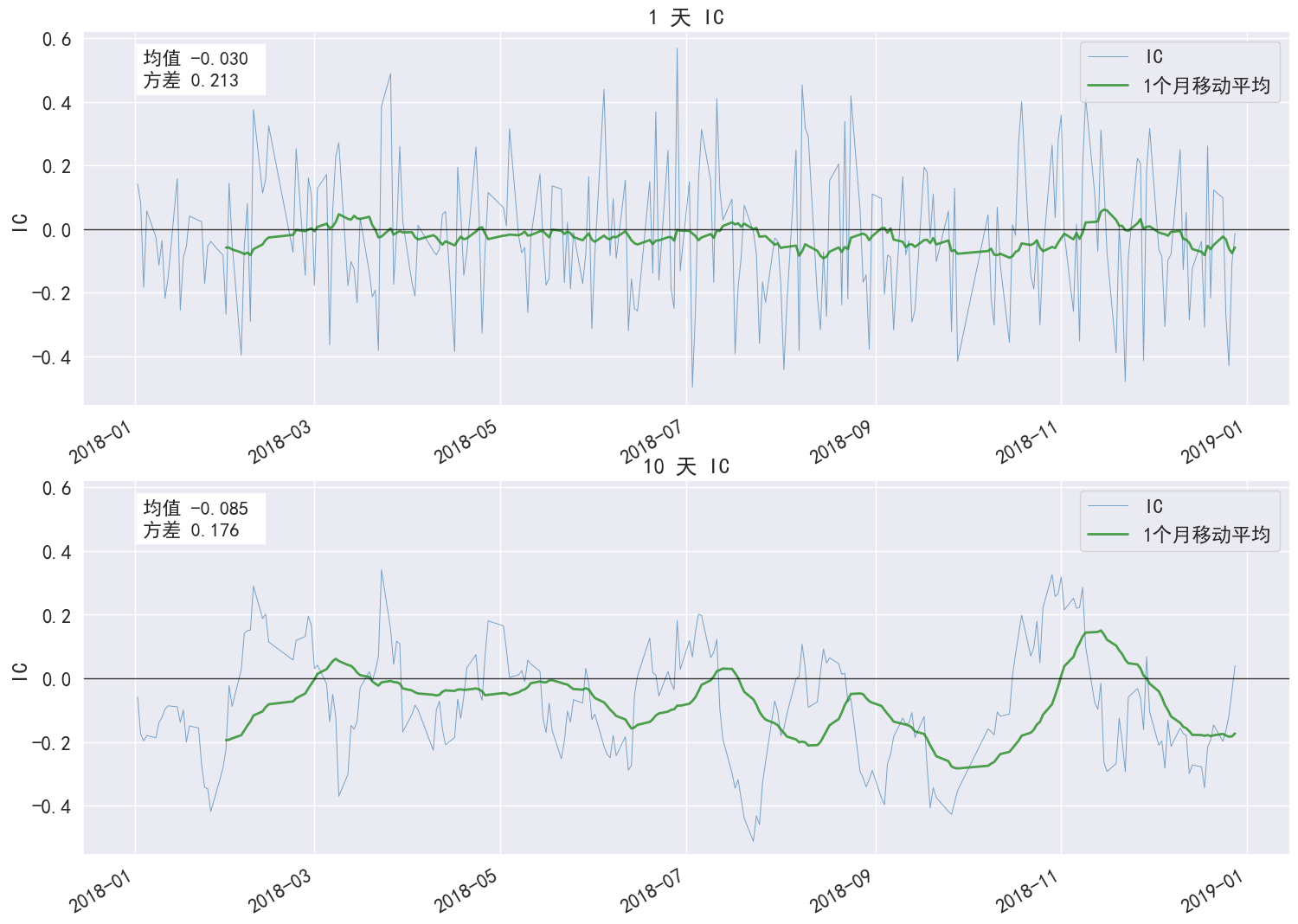
-------------------------
换手率分析
|
period_1 |
period_10 |
| Quantile 1 Mean Turnover |
0.055 |
0.222 |
| Quantile 2 Mean Turnover |
0.136 |
0.447 |
| Quantile 3 Mean Turnover |
0.206 |
0.599 |
| Quantile 4 Mean Turnover |
0.268 |
0.680 |
| Quantile 5 Mean Turnover |
0.307 |
0.730 |
| Quantile 6 Mean Turnover |
0.337 |
0.742 |
| Quantile 7 Mean Turnover |
0.326 |
0.735 |
| Quantile 8 Mean Turnover |
0.279 |
0.708 |
| Quantile 9 Mean Turnover |
0.196 |
0.593 |
| Quantile 10 Mean Turnover |
0.073 |
0.283 |
|
period_1 |
period_10 |
| Mean Factor Rank Autocorrelation |
0.991 |
0.884 |
......(图片过多,此处内容演示已省略,请参考api说明使用)
### 获取聚宽因子库数据的方法
[聚宽因子库](https://www.joinquant.com/help/api/help#name:factor_values)包含数百个质量、情绪、风险等其他类目的因子
连接jqdatasdk获取数据包,数据接口需调用聚宽 [jqdatasdk](https://www.joinquant.com/help/api/doc?name=JQDatadoc) 接口获取金融数据 ([试用注册地址](https://www.joinquant.com/default/index/sdk))
```python
# 获取因子数据:以5日平均换手率为例,该数据可以直接用于因子分析
# 具体使用方法可以参照jqdatasdk的API文档
import jqdatasdk
jqdatasdk.auth('username', 'password')
# 获取聚宽因子库中的VOL5数据
factor_data=jqdatasdk.get_factor_values(
securities=jqdatasdk.get_index_stocks('000300.XSHG'),
factors=['VOL5'],
start_date='2018-01-01',
end_date='2018-12-31')['VOL5']
```
### 将自有因子值转换成 DataFrame 格式的数据
- index 为日期,格式为 pandas 日期通用的 DatetimeIndex
- columns 为股票代码,格式要求符合聚宽的代码定义规则(如:平安银行的股票代码为 000001.XSHE)
- 如果是深交所上市的股票,在股票代码后面需要加入 .XSHE
- 如果是上交所上市的股票,在股票代码后面需要加入 .XSHG
- 将 pandas.DataFrame 转换成满足格式要求数据格式
首先要保证 index 为 DatetimeIndex 格式,一般是通过 pandas 提供的 pandas.to_datetime 函数进行转换,在转换前应确保 index 中的值都为合理的日期格式, 如 '2018-01-01' / '20180101',之后再调用 pandas.to_datetime 进行转换;另外应确保 index 的日期是按照从小到大的顺序排列的,可以通过 sort_index 进行排序;最后请检查 columns 中的股票代码是否都满足聚宽的代码定义。
```python
import pandas as pd
sample_data = pd.DataFrame(
[[0.84, 0.43, 2.33, 0.86, 0.96],
[1.06, 0.51, 2.60, 0.90, 1.09],
[1.12, 0.54, 2.68, 0.94, 1.12],
[1.07, 0.64, 2.65, 1.33, 1.15],
[1.21, 0.73, 2.97, 1.65, 1.19]],
index=['2018-01-02', '2018-01-03', '2018-01-04', '2018-01-05', '2018-01-08'],
columns=['000001.XSHE', '000002.XSHE', '000063.XSHE', '000069.XSHE', '000100.XSHE']
)
print(sample_data)
factor_data = sample_data.copy()
# 将 index 转换为 DatetimeIndex
factor_data.index = pd.to_datetime(factor_data.index)
# 将 DataFrame 按照日期顺序排列
factor_data = factor_data.sort_index()
# 检查 columns 是否满足聚宽股票代码格式
if not sample_data.columns.astype(str).str.match('\d{6}\.XSH[EG]').all():
print("有不满足聚宽股票代码格式的股票")
print(sample_data.columns[~sample_data.columns.astype(str).str.match('\d{6}\.XSH[EG]')])
print(factor_data)
```
- 将键为日期,值为各股票因子值的 Series 的 dict 转换成 pandas.DataFrame,可以直接利用 pandas.DataFrame 生成
```python
sample_data = \
{'2018-01-02': pd.Seris([0.84, 0.43, 2.33, 0.86, 0.96],
index=['000001.XSHE', '000002.XSHE', '000063.XSHE', '000069.XSHE', '000100.XSHE']),
'2018-01-03': pd.Seris([1.06, 0.51, 2.60, 0.90, 1.09],
index=['000001.XSHE', '000002.XSHE', '000063.XSHE', '000069.XSHE', '000100.XSHE']),
'2018-01-04': pd.Seris([1.12, 0.54, 2.68, 0.94, 1.12],
index=['000001.XSHE', '000002.XSHE', '000063.XSHE', '000069.XSHE', '000100.XSHE']),
'2018-01-05': pd.Seris([1.07, 0.64, 2.65, 1.33, 1.15],
index=['000001.XSHE', '000002.XSHE', '000063.XSHE', '000069.XSHE', '000100.XSHE']),
'2018-01-08': pd.Seris([1.21, 0.73, 2.97, 1.65, 1.19],
index=['000001.XSHE', '000002.XSHE', '000063.XSHE', '000069.XSHE', '000100.XSHE'])}
import pandas as pd
# 直接调用 pd.DataFrame 将 dict 转换为 DataFrame
factor_data = pd.DataFrame(data).T
print(factor_data)
# 之后请按照 DataFrae 的方法转换成满足格式要求数据格式
```