# DataMining
**Repository Path**: zhu-ronghui/data-mining
## Basic Information
- **Project Name**: DataMining
- **Description**: 数据挖掘--基于TCGA的癌症RNA表达数据挖掘与分析
- **Primary Language**: Python
- **License**: Not specified
- **Default Branch**: master
- **Homepage**: None
- **GVP Project**: No
## Statistics
- **Stars**: 0
- **Forks**: 0
- **Created**: 2024-04-15
- **Last Updated**: 2024-04-19
## Categories & Tags
**Categories**: Uncategorized
**Tags**: None
## README
# [数据挖掘]对TCGA数据库的五种癌症的数据挖掘与分析
## 1.目的
通过实际数据集上的编程实践,掌握高维数据常用的数据探索与可视化技术,观察和理解“维数灾难”问题的涵义、以及相似性度量和维归约的重要性。
## 2.数据
癌症基因图谱(The Cancer Genome Atlas Program, TCGA)数据库
(https://portal.gdc.cancer.gov/repository)
中5 种不同类型癌症:膀胱移行细胞癌、乳腺浸润性癌、脑低级别胶质瘤、肺腺癌和肺鳞状细胞癌(缩写为BLCA,BRCA,LGG, LUAD 和LUSC, 每种为一个数据集)病例的RNA 转录组
(RNA-seq)数据。
数据下载说明:
1. 打开gdc官网,新建一个project,将'TCGA-BLCA','TCGA-BRCA','TCGA-LGG','TCGA-LUAD'和'TCGA-LUSC'添加进当前工程中。
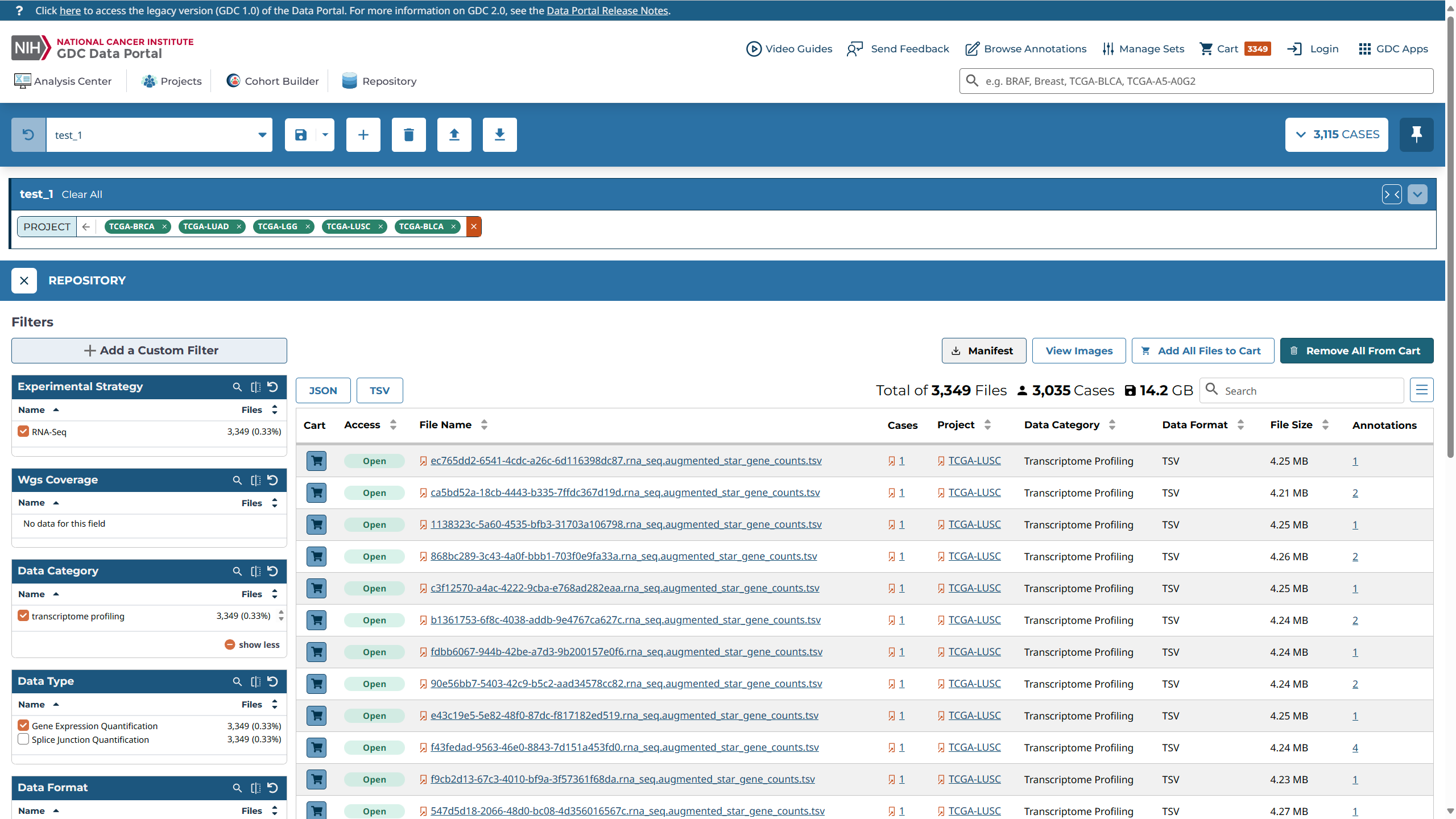
2. 打开gdc/repository,按如下的方式勾选(a)Data Category: transcriptome profiling、(b)Data
Type: Gene Expression Quantification、(c)Experimental Strategy: RNA-Seq。最后一共筛选出有14.2GB的数据符合我们的要求。
**在这里需要注意的是:由于gdc官网更新到了2.0,因此老版界面中RNA- Workflow Type: HTSeq - FPKM-UQ选项不存在了,推测原因为老版的.txt文件可以只单独地导出FPKM-UQ数据,而在新版的.tsv文件中将unstranded、stranded_first 、stranded_second、 tpm_unstranded 、 fpkm_unstranded 和fpkm_uq_unstranded全部合并在了同一个文件中。**
3. Add All Files to Cart,将全部数据添加到购物车,然后打开购物车选择下载。经过实践,由于数据集体积超过了5GB,使用gdc提供的那个带ui的下载程序是不容易成功的(至少本人没成功),所以我们选择下载gdc_samplesheet.tsv文件(该文件保存了各个病例的相关信息)和gdc_manifest文件(该文件用于后续下载数据集)。
4. 下载gdc-client.exe,保存到本地,在该目录下(如果想不在目录下调用它,则需要添加环境变量)打开cmd或powershell在该目录下运行:
```powershell
.\gdc-client.exe download -m gdc_manifest.2024-04-07.txt
```
5. 数据集的下载过程较长,建议有一个稳定的网络环境。
 ## 3.数据处理
### 3.1 数据分类
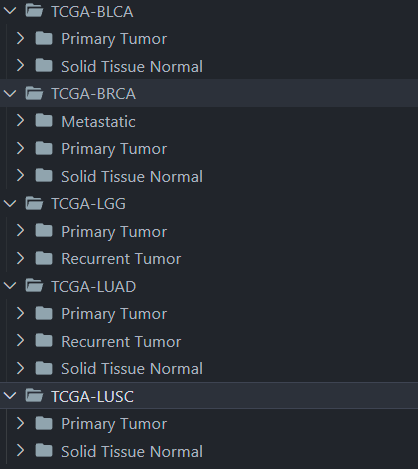
在完成上一步的数据下载之后,我们会得到三千多个文件夹,这时候来自五个癌症的数据都是混杂在一起的,因此我们使用程序先把五种癌症的RNA数据分门别类的放好。在这里我选择了使用sample type对每种癌症的数据集进行分类,每种癌症都不太相同,但大致都有两类solid tissue normal(实体组织正常,也就是对照组)和Primary Tumor(原发性肿瘤)。
## 3.数据处理
### 3.1 数据分类
在完成上一步的数据下载之后,我们会得到三千多个文件夹,这时候来自五个癌症的数据都是混杂在一起的,因此我们使用程序先把五种癌症的RNA数据分门别类的放好。在这里我选择了使用sample type对每种癌症的数据集进行分类,每种癌症都不太相同,但大致都有两类solid tissue normal(实体组织正常,也就是对照组)和Primary Tumor(原发性肿瘤)。
 代码:
```python
import os
import shutil
# 定义文件夹路径
tcga_folder = 'TCGA' # 包含所有数据的文件夹
# 读取samplesheet.tsv文件
sample_sheet_path = 'gdc_sample_sheet.2024-04-07.tsv'
with open(sample_sheet_path, 'r') as file:
lines = file.readlines()
count =0
# 遍历
for line in lines:
count+=1
# 跳过标题行
if count==1:
continue
# 分割每一行的数据
parts = line.strip().split('\t')
file_id = parts[0] # 文件ID
project_id = parts[4] # 项目ID
sample_type = parts[7] # 样本类型
# 构建源文件夹路径
source_folder = os.path.join(tcga_folder, file_id)
# 构建目标文件夹路径
target_folder = os.path.join(project_id, sample_type)
os.makedirs(target_folder, exist_ok=True) # 确保目标文件夹存在
# 移动文件夹
shutil.move(source_folder, target_folder)
print(f'Moved {source_folder} to {target_folder}')
print(count)
```
### 3.2 数据预处理(聚集、清洗、标准化)
1. 观察原始数据的可发现第一列为gene_id,最后一列为fpkm_uq_unstranded(未校正的每千个碱基的片段数),且前四行都是表达量的统计信息,因此第四行以后是我们需要使用的数据。
2. 由于此时每个癌症样本的RNA数据独立存在于.tsv文件中,不利于后续处理。因此我们需要提取每个RNA-seq文件的最后一列(前四行不包括),并把它们拼接起来,形成一个数据矩阵,完成**数据聚集**。
3. 观察原始数据可知,有大量基因表达量为0,因此选择做**数据清洗**:对于每一个数据集,在 6 万多个 RNA 中,如果某RNA在一半以上的病例中没有表达(数值为0),则将其丢弃(最终剩余3 万个左右的基因用于分析)
4. 对于完成前面处理的数据而已,我们还要做数据标准化$x = log_{10}(x + 1)$,这样可以保证各个数据大致在一个数量级,方便后续的处理。
使用一个函数来完成上述过程,并把结果存储在.tsv文件中,方便后续调用:
```python
def pre_process(file_dir):
temp_df = pd.DataFrame()
cases = find_cases(file_dir)
for i, case in enumerate(tqdm(cases)):
df_test = pd.read_csv(case[0],sep='\t',comment='#',header=0,index_col=0)
temp_df = pd.concat([temp_df,df_test.iloc[4:,7]],axis=1,ignore_index=False)
# temp_df = temp_df.transpose()
print(temp_df,temp_df.shape)
# return
index_list = []
for i in range(temp_df.shape[0]):
number = dict(temp_df.iloc[i].value_counts(normalize=True)) # 统计第i行所有元素的个数(以百分比形式显示)
number_default_value = defaultdict(int,number) # 为防止字典里没有KEY0.0,从而使用defaultdict
if number_default_value[0.0] > 0.5: # 如果某RNA在一半以上的病例中没有表达(数值为0),则将其丢弃
index_list.append(i) # 将对应的行号放入列表中
# 删除指定行(index_list里的行数)
temp_df = temp_df.drop(temp_df.index[index_list])
temp_df = temp_df.apply(lambda x : np.log10(x+1)) #对数标准化
new_column_names = [str(i) for i in range(temp_df.shape[1])]
temp_df.columns = new_column_names
print(temp_df,temp_df.shape)
temp_df.to_csv(f'{file_dir}.tsv',sep='\t')
return
```
## 4.数据的初步探索和可视化
### 4.1 分别画出五个数据集的的数据矩阵图(data matrix)
> 数据集的数据矩阵图(也称为热图或矩阵图)是一种可视化工具,用于展示数据集中多个变量之间的关系,或者展示数据集中多个样本之间的相似性和差异性。在这种图表中,数据被组织成一个矩阵的形式,矩阵中的每个单元格代表一个变量(或样本)与另一个变量(或样本)之间的关系或比较。
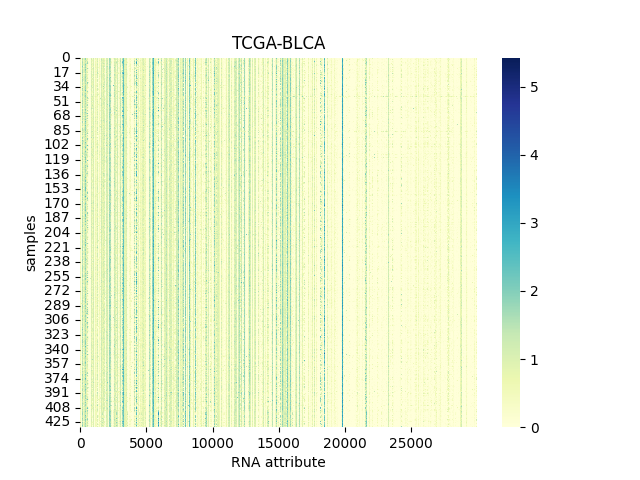
以下分别为TCGA-BLCA, TCGA-BRCA, TCGA-LGG, TCGA-LUAD 和TCGA-LUSC数据集的数据矩阵图。
#### 4.1.1 TCGA-BLCA
代码:
```python
import os
import shutil
# 定义文件夹路径
tcga_folder = 'TCGA' # 包含所有数据的文件夹
# 读取samplesheet.tsv文件
sample_sheet_path = 'gdc_sample_sheet.2024-04-07.tsv'
with open(sample_sheet_path, 'r') as file:
lines = file.readlines()
count =0
# 遍历
for line in lines:
count+=1
# 跳过标题行
if count==1:
continue
# 分割每一行的数据
parts = line.strip().split('\t')
file_id = parts[0] # 文件ID
project_id = parts[4] # 项目ID
sample_type = parts[7] # 样本类型
# 构建源文件夹路径
source_folder = os.path.join(tcga_folder, file_id)
# 构建目标文件夹路径
target_folder = os.path.join(project_id, sample_type)
os.makedirs(target_folder, exist_ok=True) # 确保目标文件夹存在
# 移动文件夹
shutil.move(source_folder, target_folder)
print(f'Moved {source_folder} to {target_folder}')
print(count)
```
### 3.2 数据预处理(聚集、清洗、标准化)
1. 观察原始数据的可发现第一列为gene_id,最后一列为fpkm_uq_unstranded(未校正的每千个碱基的片段数),且前四行都是表达量的统计信息,因此第四行以后是我们需要使用的数据。
2. 由于此时每个癌症样本的RNA数据独立存在于.tsv文件中,不利于后续处理。因此我们需要提取每个RNA-seq文件的最后一列(前四行不包括),并把它们拼接起来,形成一个数据矩阵,完成**数据聚集**。
3. 观察原始数据可知,有大量基因表达量为0,因此选择做**数据清洗**:对于每一个数据集,在 6 万多个 RNA 中,如果某RNA在一半以上的病例中没有表达(数值为0),则将其丢弃(最终剩余3 万个左右的基因用于分析)
4. 对于完成前面处理的数据而已,我们还要做数据标准化$x = log_{10}(x + 1)$,这样可以保证各个数据大致在一个数量级,方便后续的处理。
使用一个函数来完成上述过程,并把结果存储在.tsv文件中,方便后续调用:
```python
def pre_process(file_dir):
temp_df = pd.DataFrame()
cases = find_cases(file_dir)
for i, case in enumerate(tqdm(cases)):
df_test = pd.read_csv(case[0],sep='\t',comment='#',header=0,index_col=0)
temp_df = pd.concat([temp_df,df_test.iloc[4:,7]],axis=1,ignore_index=False)
# temp_df = temp_df.transpose()
print(temp_df,temp_df.shape)
# return
index_list = []
for i in range(temp_df.shape[0]):
number = dict(temp_df.iloc[i].value_counts(normalize=True)) # 统计第i行所有元素的个数(以百分比形式显示)
number_default_value = defaultdict(int,number) # 为防止字典里没有KEY0.0,从而使用defaultdict
if number_default_value[0.0] > 0.5: # 如果某RNA在一半以上的病例中没有表达(数值为0),则将其丢弃
index_list.append(i) # 将对应的行号放入列表中
# 删除指定行(index_list里的行数)
temp_df = temp_df.drop(temp_df.index[index_list])
temp_df = temp_df.apply(lambda x : np.log10(x+1)) #对数标准化
new_column_names = [str(i) for i in range(temp_df.shape[1])]
temp_df.columns = new_column_names
print(temp_df,temp_df.shape)
temp_df.to_csv(f'{file_dir}.tsv',sep='\t')
return
```
## 4.数据的初步探索和可视化
### 4.1 分别画出五个数据集的的数据矩阵图(data matrix)
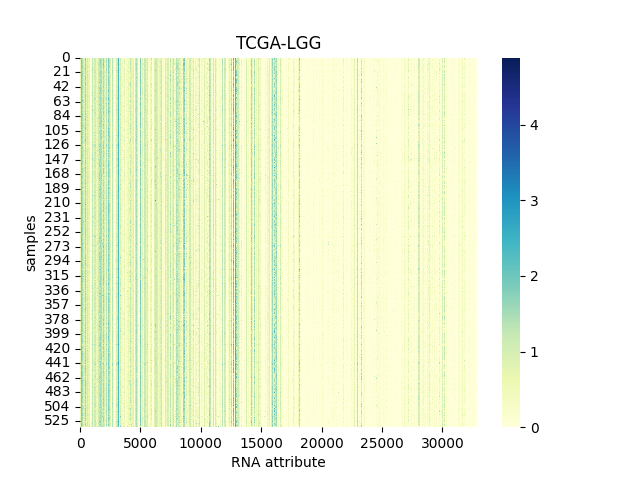
> 数据集的数据矩阵图(也称为热图或矩阵图)是一种可视化工具,用于展示数据集中多个变量之间的关系,或者展示数据集中多个样本之间的相似性和差异性。在这种图表中,数据被组织成一个矩阵的形式,矩阵中的每个单元格代表一个变量(或样本)与另一个变量(或样本)之间的关系或比较。
以下分别为TCGA-BLCA, TCGA-BRCA, TCGA-LGG, TCGA-LUAD 和TCGA-LUSC数据集的数据矩阵图。
#### 4.1.1 TCGA-BLCA
 #### 4.1.2 TCGA-BRCA
#### 4.1.2 TCGA-BRCA
 #### 4.1.3 TCGA-LGG
#### 4.1.3 TCGA-LGG
 #### 4.1.4 TCGA-LUAD
#### 4.1.4 TCGA-LUAD
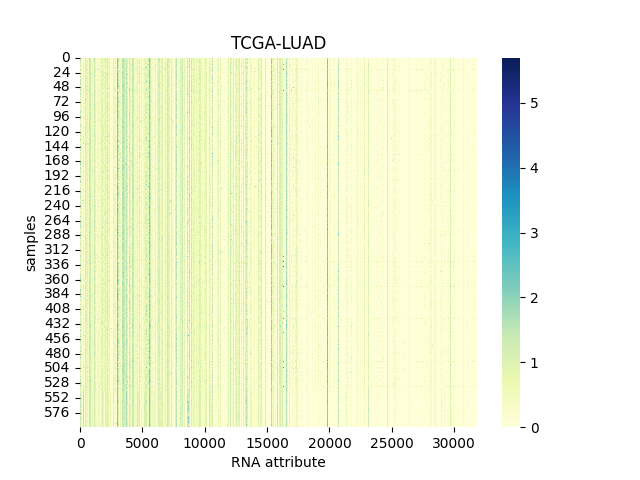 #### 4.1.5 TCGA-LUSC
#### 4.1.5 TCGA-LUSC
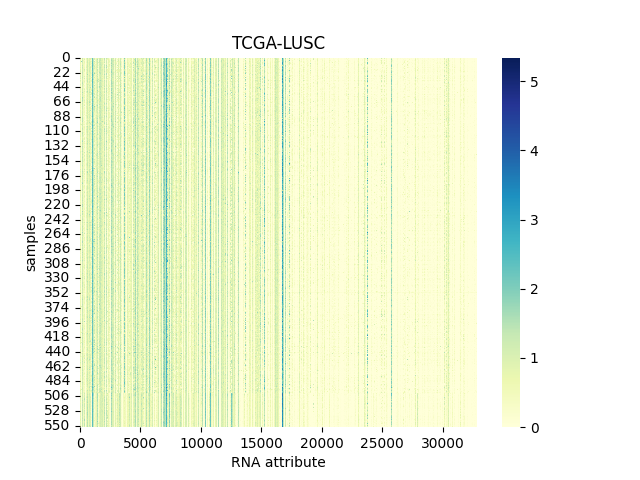 ### 4.2 任选10 个RNA 维度(属性),分别画出每个维度的直方图和盒状图,并进行跨数据集比较。
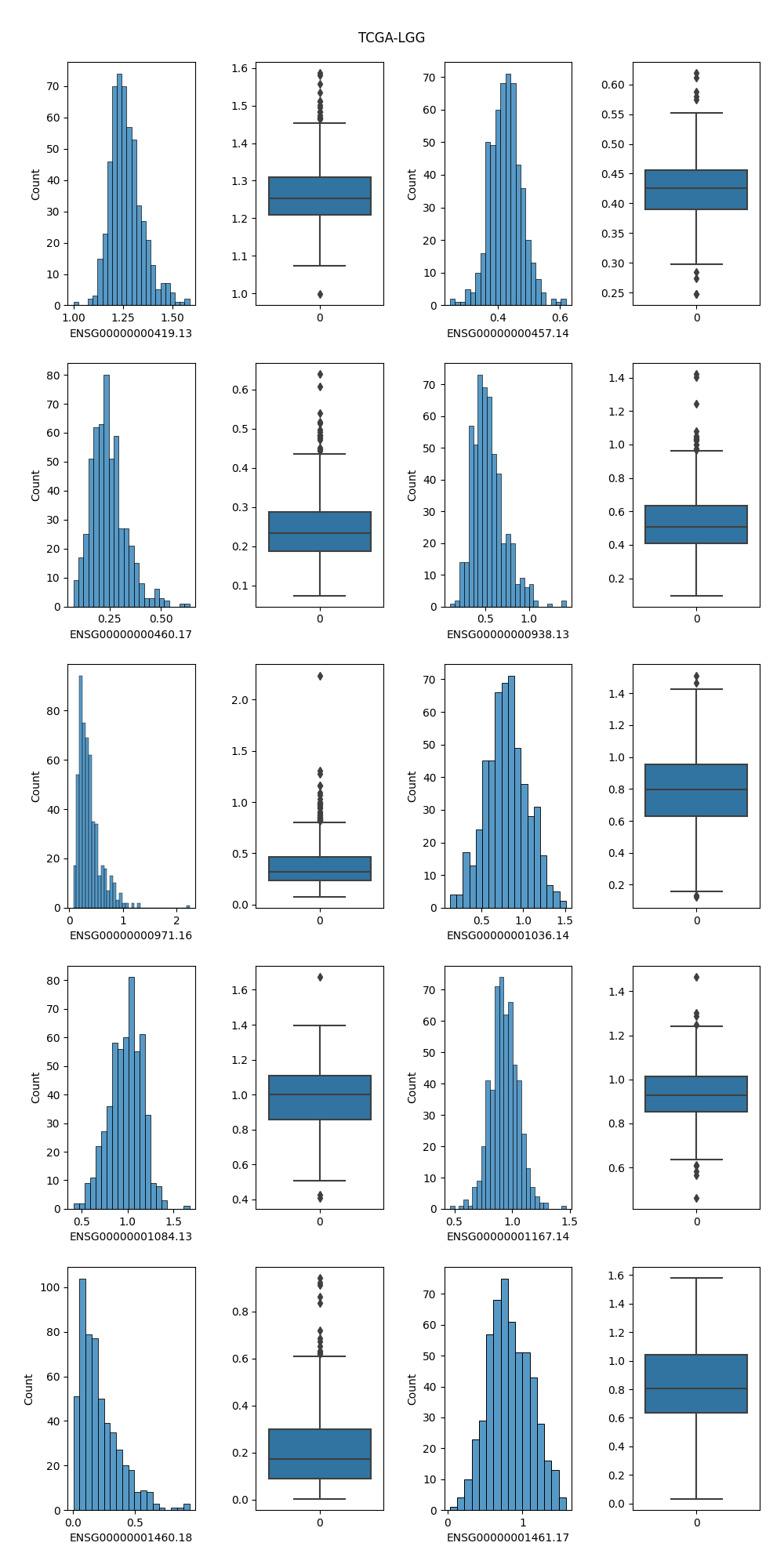
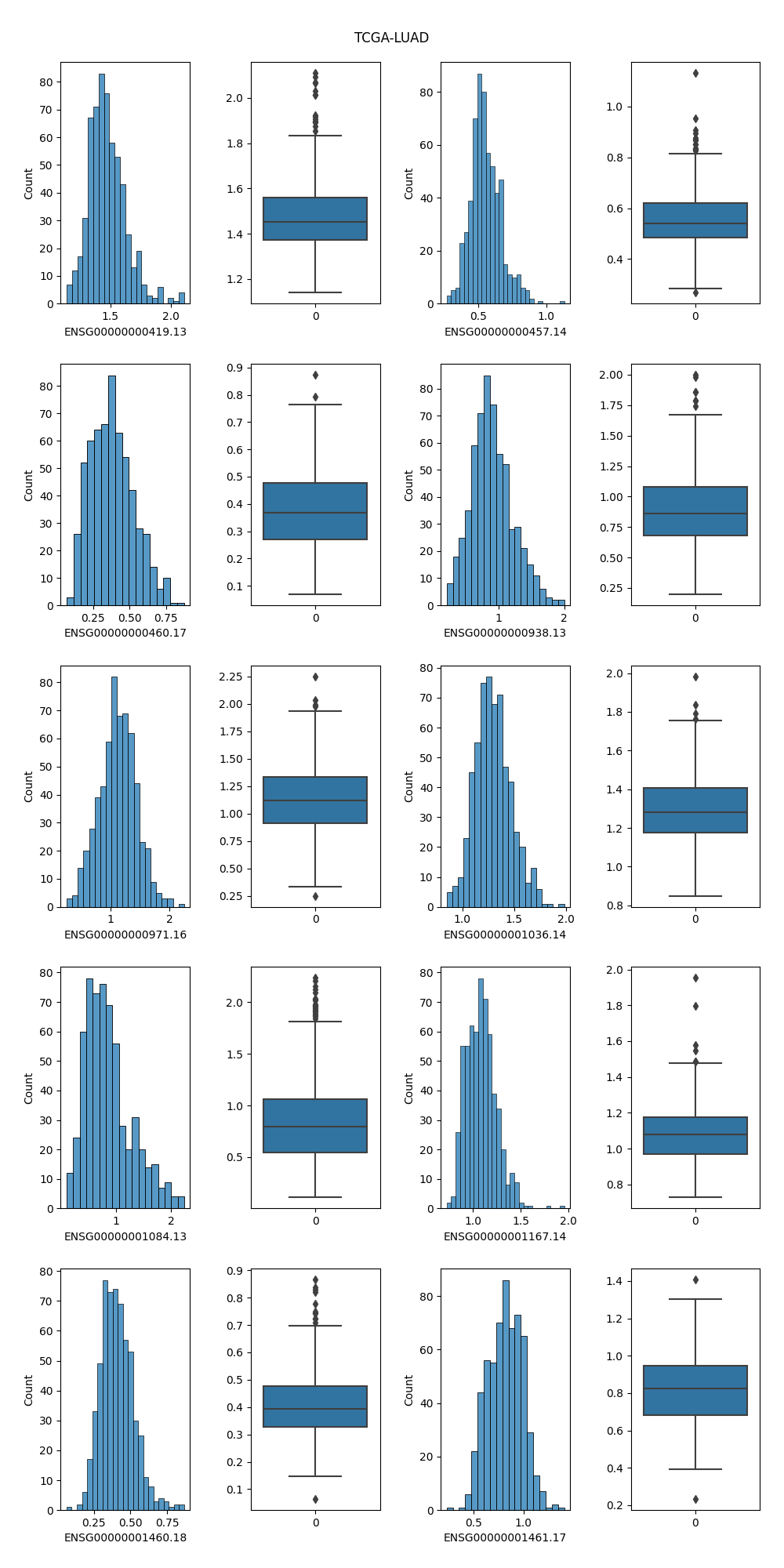
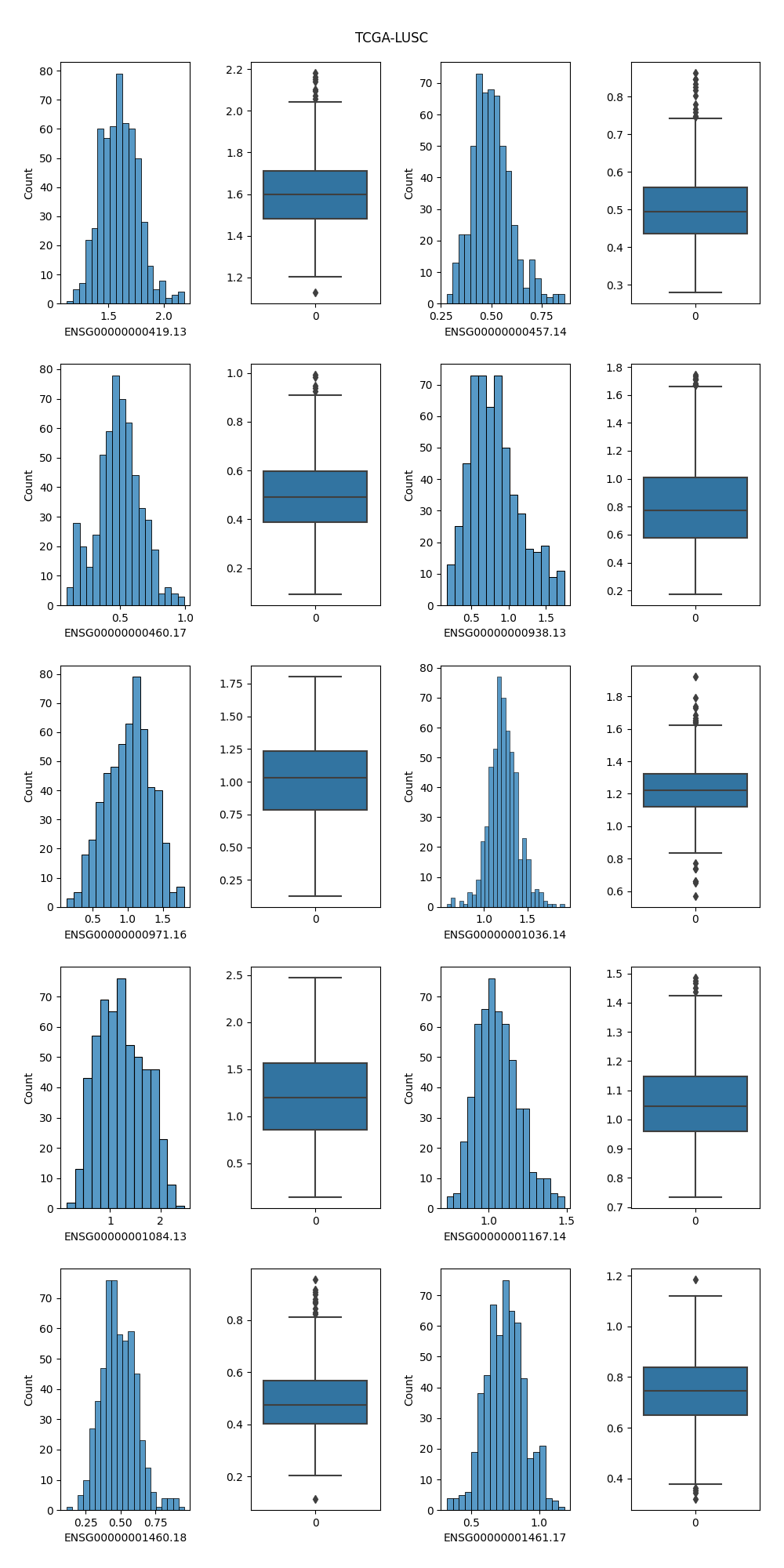
经过观察我发现,基因ID为:ENSG00000000419.13、ENSG00000000457.14、ENSG00000000460.17、ENSG00000000938.13、ENSG00000000971.16、ENSG00000001036.14、ENSG00000001084.13、ENSG00000001167.14、ENSG00000001460.18和ENSG00000001461.17的基因在五种癌症中都有较高的表达了,不妨选取这十个RNA维度并绘制相关图像进行比较分析。
#### 4.2.1 TCGA-BLCA
### 4.2 任选10 个RNA 维度(属性),分别画出每个维度的直方图和盒状图,并进行跨数据集比较。
经过观察我发现,基因ID为:ENSG00000000419.13、ENSG00000000457.14、ENSG00000000460.17、ENSG00000000938.13、ENSG00000000971.16、ENSG00000001036.14、ENSG00000001084.13、ENSG00000001167.14、ENSG00000001460.18和ENSG00000001461.17的基因在五种癌症中都有较高的表达了,不妨选取这十个RNA维度并绘制相关图像进行比较分析。
#### 4.2.1 TCGA-BLCA
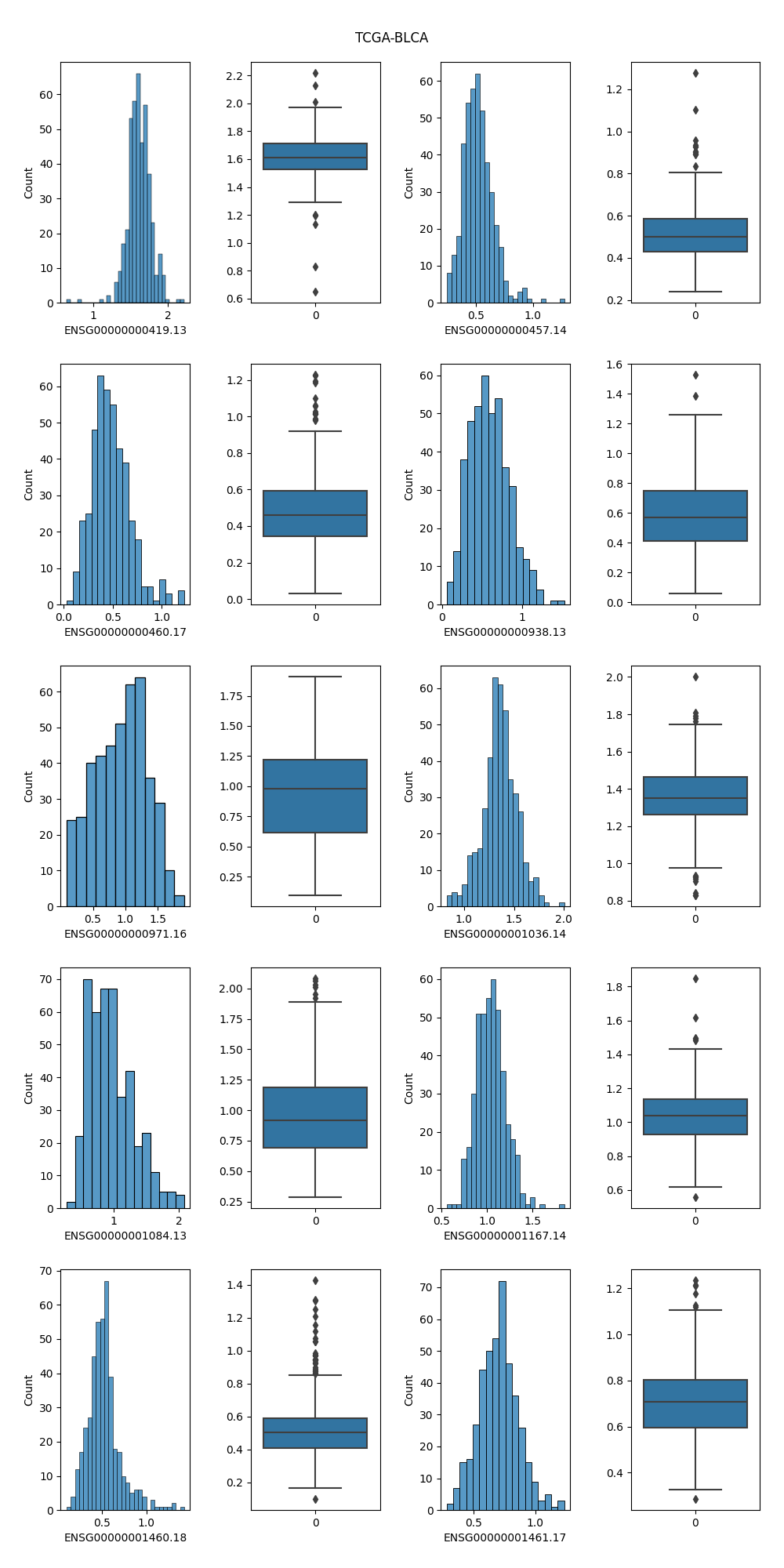 #### 4.2.2 TCGA-BRCA
#### 4.2.2 TCGA-BRCA
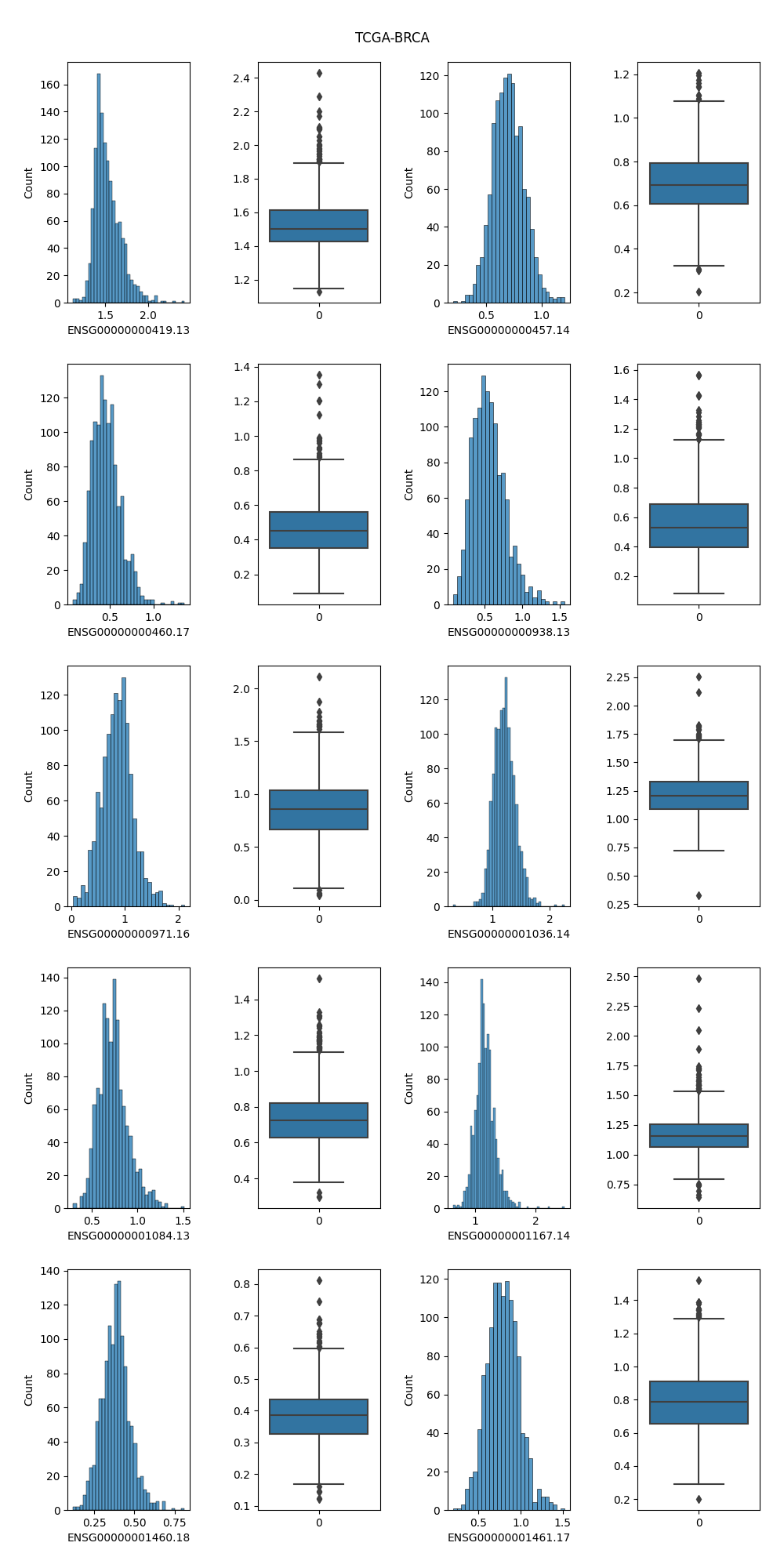 #### 4.2.3 TCGA-LGG
#### 4.2.3 TCGA-LGG
 #### 4.2.4 TCGA-LUAD
#### 4.2.4 TCGA-LUAD
 #### 4.2.5 TCGA-LUSC
#### 4.2.5 TCGA-LUSC
 #### 4.2.6 分析
1. 直方图清晰地反映了该属性的表达值的分布情况,可以通过直方图的高度方便地看出数据的绝对频率(计数)或相对频率(概率密度)
2. 盒状图可以从宏观的角度看出属性的分布,并且直观明了地识别数据中的异常值(在上下限以外的菱形符号就表示异常值);并且盒状图突出显示了数据的**中位数**和**四分位数间距**,有助于了解数据的中心趋势。
3. 基因ENSG00000001460.18在TCGA-LGG这个类别的样本相较于其他四种癌症,表达量比较低,从直方图中可看出它在LGG数据集样本中表达量分布大致在0附近;观察盒状图可发现,该基因表达量中位数在LGG约为0.2,而在其他四个癌症中约为0.4,可以初步认为该基因在LGG数据集中相较于其他数据集不同。
### 4.3 采用t-SNE方法将数据集降维至2D 进行可视化。
1. 在之前的工作中,我们已经将各个数据集的样本数据聚集在.tsv文件中,因此我选择读取.tsv中的数据存取在pd.DataFrame中,并作转置,转置后的数据矩阵形状为(n_samples, n_rna_component)
2. 由于每个样本的RNA-seq的维度有大约30000,因此我选择使用t-sne对数据进行降维至2维进行可视化。
3. 在降维的过程中我们还可以根据各个数据集的sample type的不同,对不同的点进行不同染色,这样可以更方便地观察出不同类样本聚集成的簇的不同。我们可以借助DataFrame的索引来进行判断与过滤,得到样本的类别。
```python
#文件所属的病例的类型--sample type、
samplesheet_df[samplesheet_df['File Name'] == file.split('\\')[-1]]['Sample Type'].item()
```
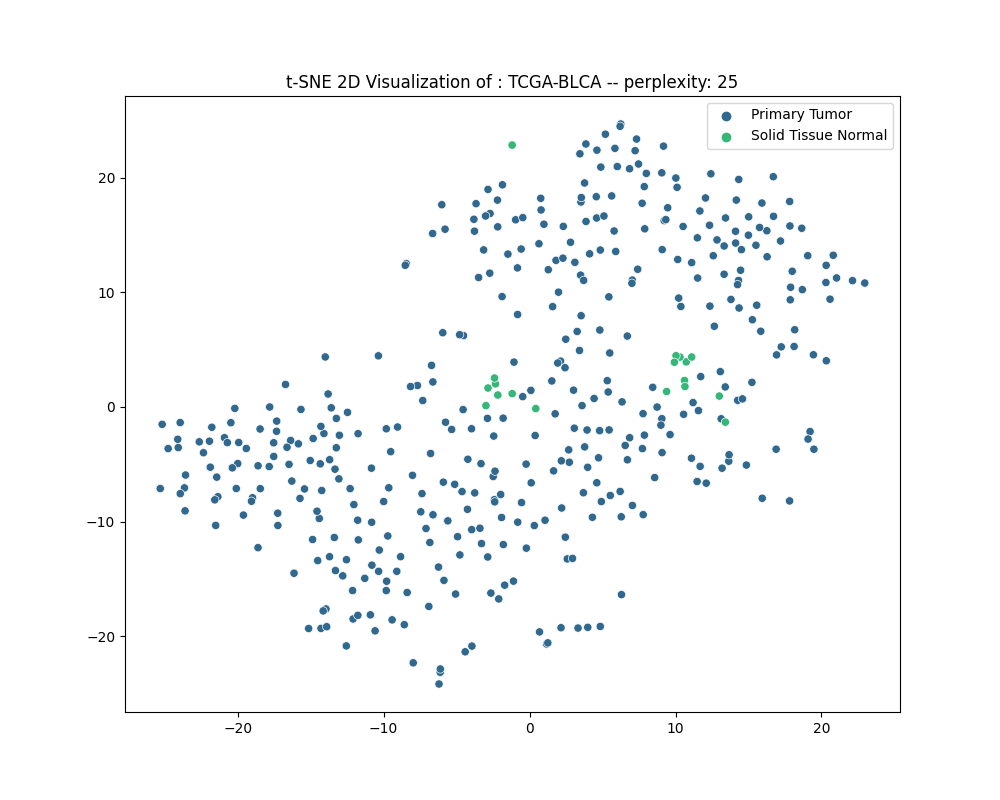
4. 由于t-nse方法的学习率、困惑度(*perplexity*)都可能影响降维的效果。而根据文献推荐,困惑度的选择在5-50为佳,经过本人的实验,选择perplexity = 25或许会有比较好的效果。
以下便得到了,五个数据集的2D可视化图像(样本点颜色取决于样本类型):
#### 4.3.1 TCGA-BLCA
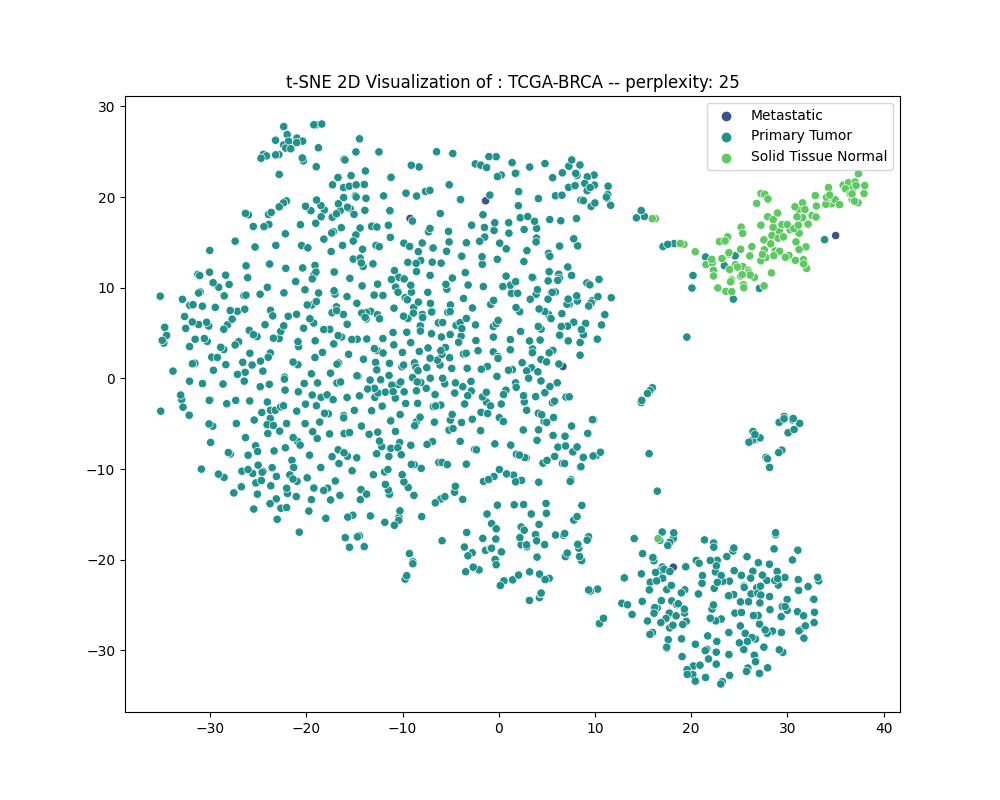
#### 4.3.2 TCGA-BRCA
#### 4.3.3 TCGA-LGG

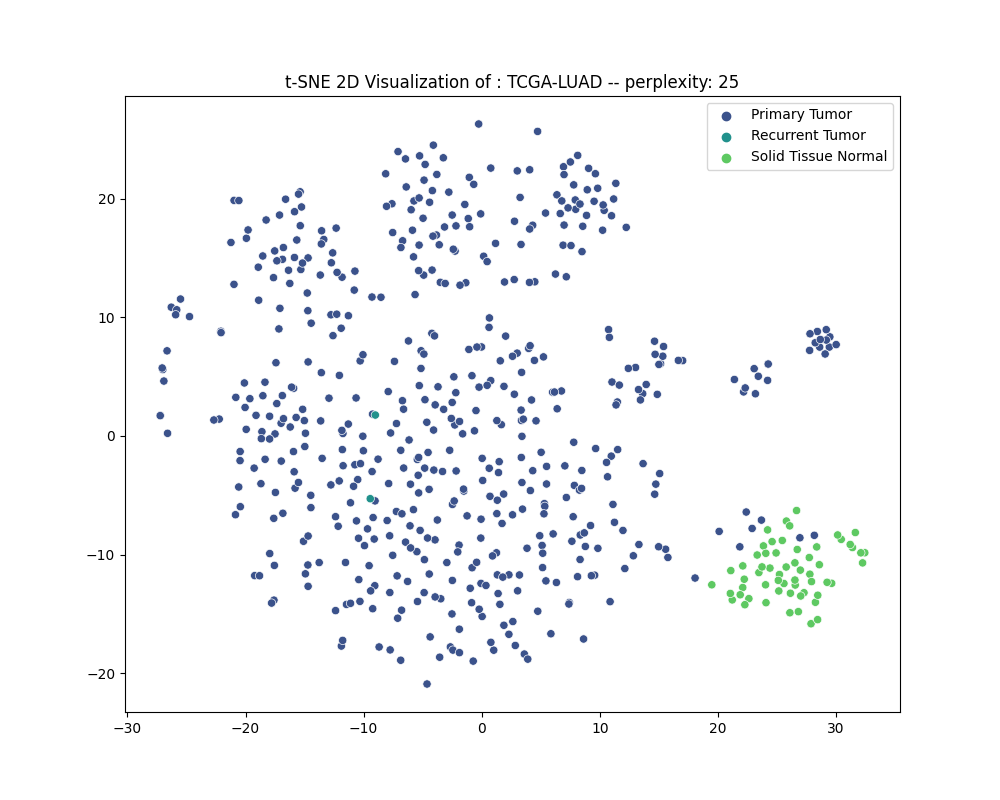
#### 4.3.4 TCGA-LUAD
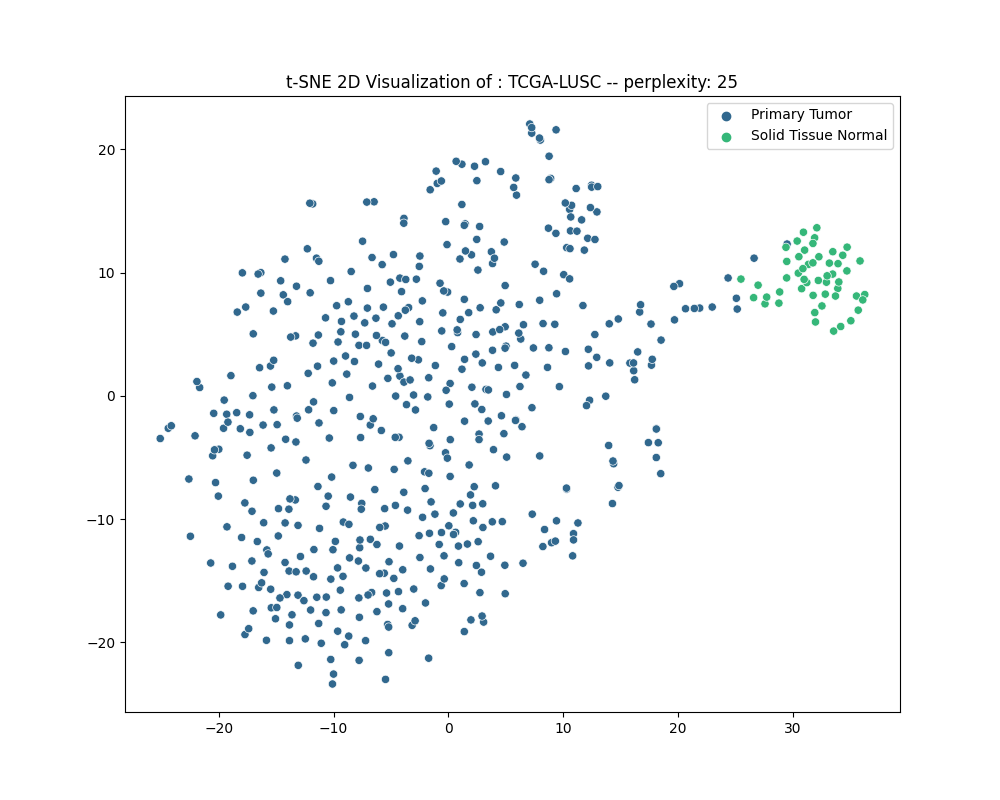
#### 4.3.5 TCGA-LUSC
#### 4.3.6 分析
通过可视化结果可以发现:
1. 除了在**BCLA**数据集中,Solid Tissue Normal——实体正常组织都能聚合在一个簇中,**并与癌症组织分开**。
2. Recurrent Tumor,复发型癌症的样本与原发癌症的样本常常混杂在一起,较难分开。
3. 尽管降维后的数据可视化图中的样本簇之间的距离并不能反映真实的样本距离,但可以认为癌症组织的RNA表达和正常组织的RNA表达确实存在差异,一定程度上可以被分隔开。
## 5. 相似性度量
分别采用:(a)欧式距离、(b)马氏距离(Mahalanobis distance)、(c)余弦距离、(d)Pearson 相关系数、(e)测地距离(geodesic distance)、(f)土机距离(Earth Mover's Distance, EMD)等6 种常见的距离(相似性)度量,计算数据对象之间的两两相似性,画出相似性矩阵(similarity matrix)。为了能反映出数据的内在模式,应先对数据进行初步聚类,将同簇的数据组织在一起。为此,可采用k-means 或其它方法在t-SNE 降维后的低维空间进行聚类。考虑做以下处理:
1. 使用t-SNE方法将五个数据集的数据矩阵降维到2维,并把数据矩阵储存在.tsv文件中
2. 利用k-means聚类算法对降低到2维的样本数据进行聚类,并根据聚类结果对数据集进行排序,使得同类数据聚集。
### 5.1 聚类与排序
在此之前我们先取k值为1~11,分别对五个数据集进行聚类,得到WCSS与K值的关系图,用于选取合适的k值。
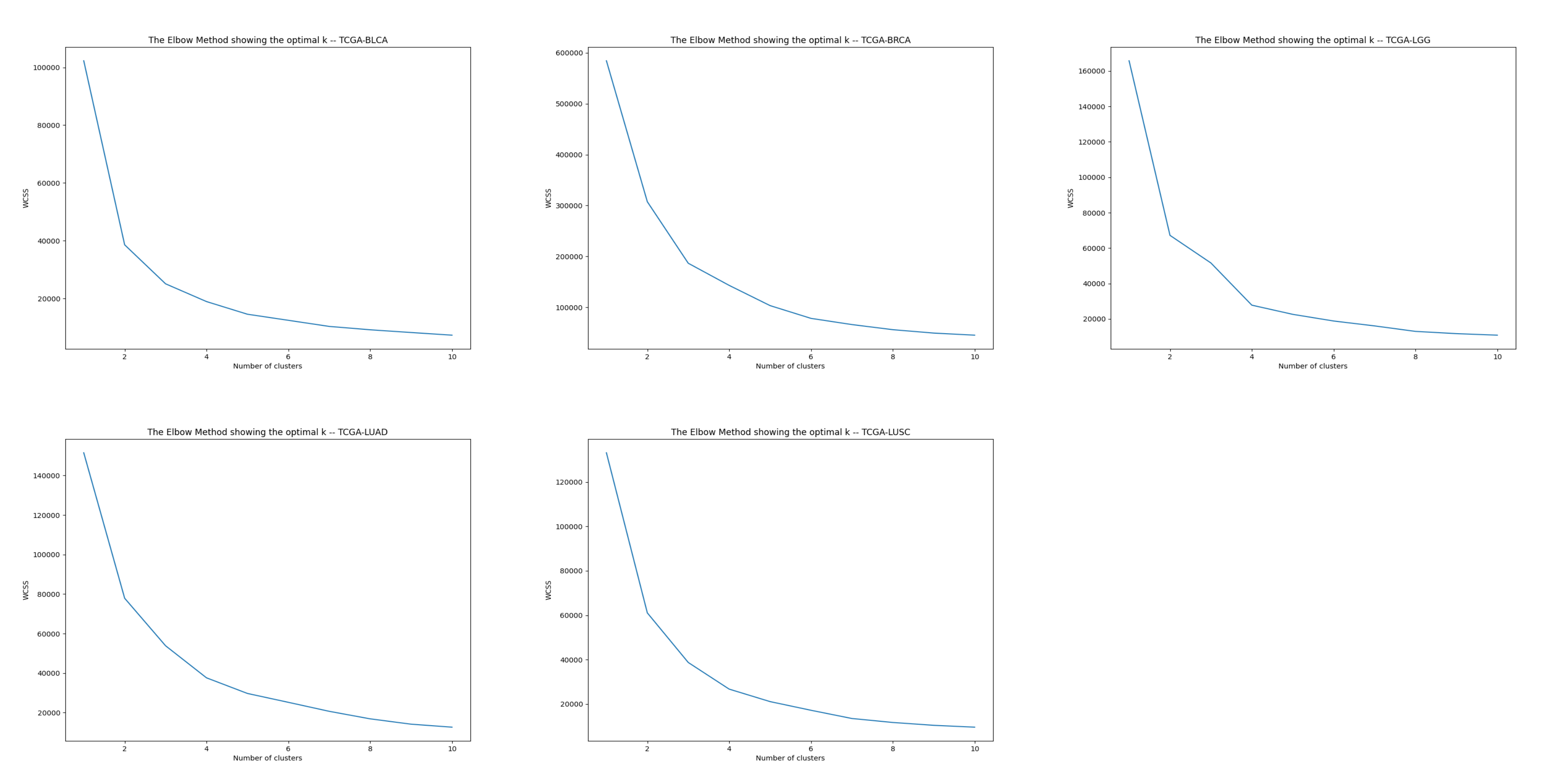
选取好合适的k值后,我们把各自的k值存储在字典中,作为后面聚类的依据。聚类并排序完成后便可以计算相似度矩阵了。
### 5.2 原始数据的相似度矩阵
这里主要有2个点我没做好:
1. 这么大的数据矩阵,计算马氏距离和推土机距离距离的时间复杂度和空间复杂度都是很大的(尤其是马氏距离涉及到计算协方差矩阵,时间复杂度至少是n^2,对于高维情况下来说这是不敢想象的),因此在未降维的情况下,对于大数据集的数据矩阵比如BRCA的数据矩阵,高达(1200,30000),这样的数据量是**非常大**的。
2. 在计算各个数据集的马氏距离,我的笔电16G内存几乎跑满了也没法出图,经过实验计算到了后期性能瓶颈已经在于内存读取而不是cpu,几个小时不出图是很正常的。本人也查了些资料,也许可以利用Python的cudf利用gpu显存和cuda核心参与计算,可能有一定改善,但时间和技术所限,没有再试验下去了。
因此,下面的相似度矩阵将缺少部分的图。
#### 5.2.1 TCGA-BLCA

#### 5.2.2 TCGA-BRCA
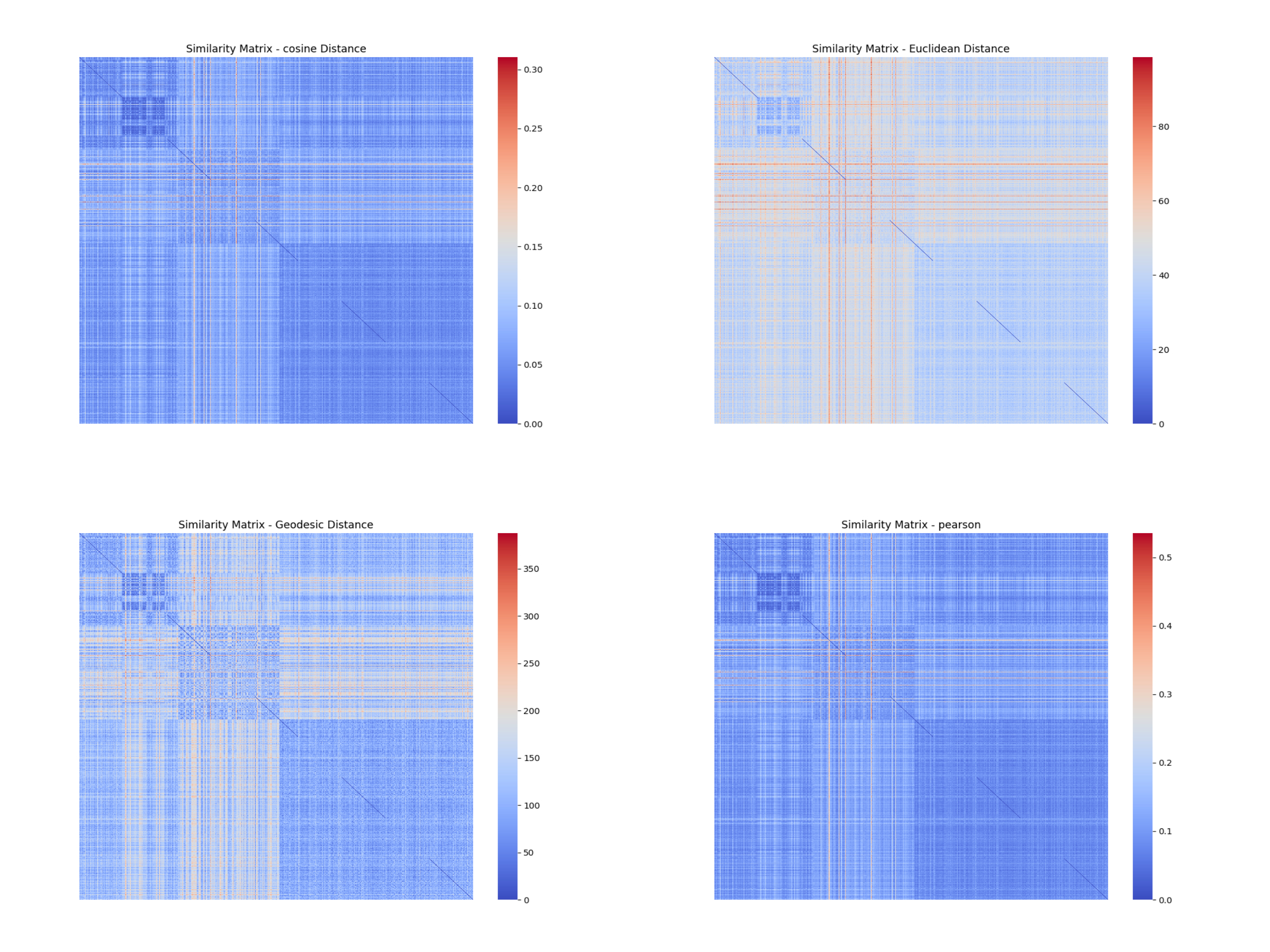
#### 5.2.3 TCGA-LGG
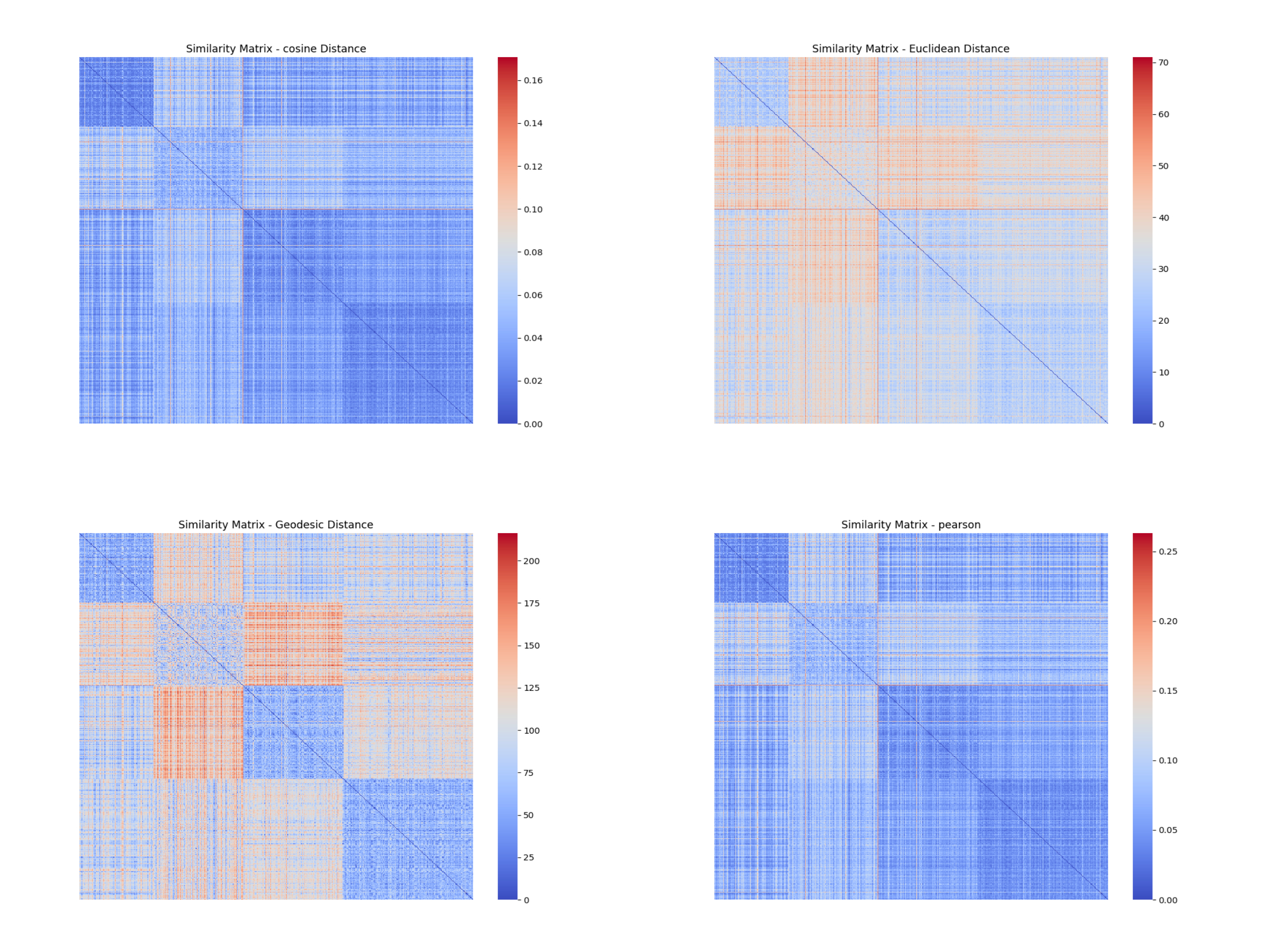
#### 5.2.4 TCGA-LUAD

#### 5.2.5 TCGA-LUSC
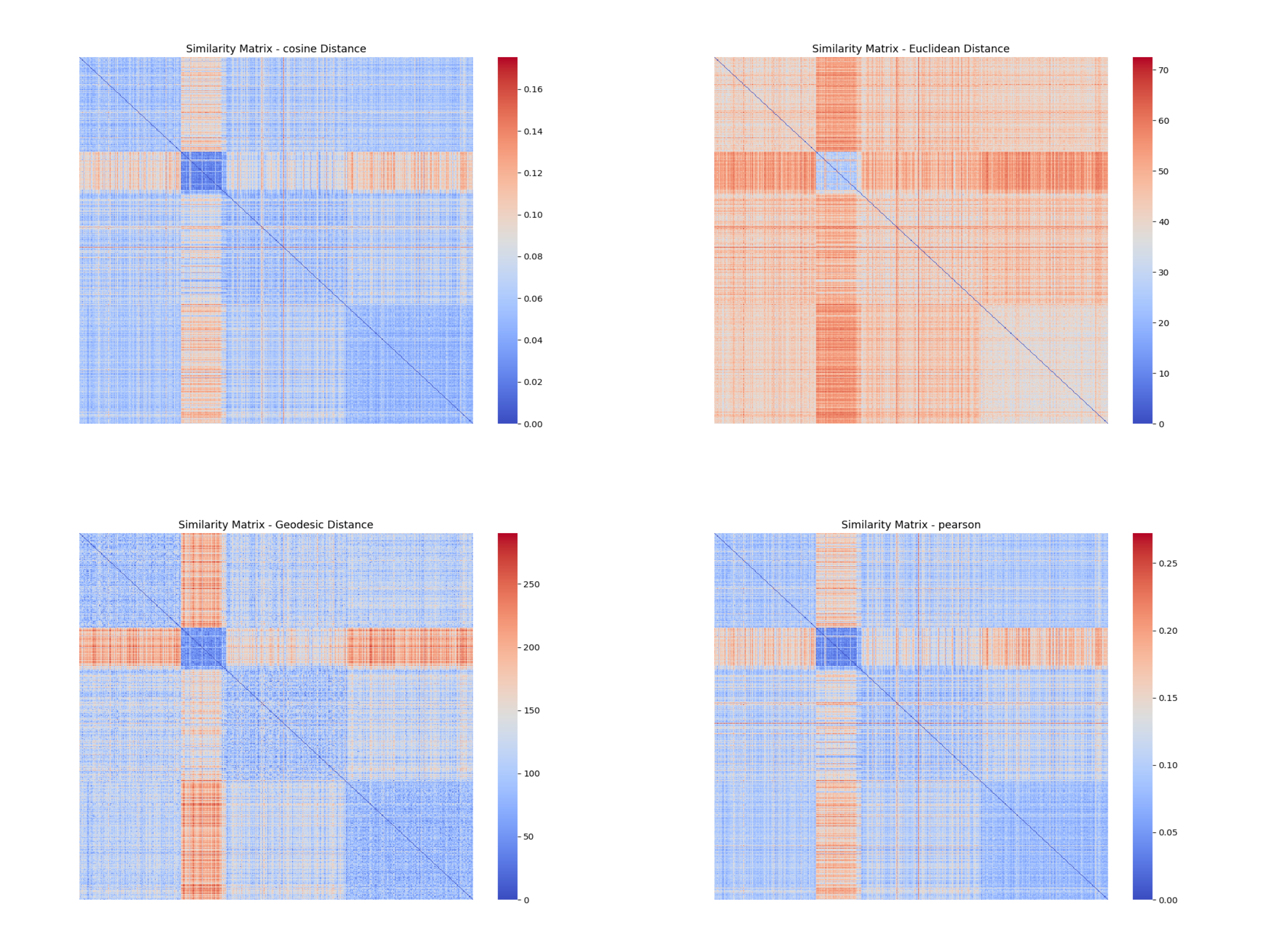
#### 5.2.6 分析
从原始数据的相似度矩阵可以看出:
- 在高维情况下,余弦距离、欧式距离和皮尔逊相关距离区分不同簇的能力不强,不同分块之间的颜色有时几乎并无差别,都为蓝色。
- 距离矩阵容易被**个别样本或噪声**影响,导致距离的值变得极大,在热图上表现为鲜艳的红色。
## 6.维归约
### 6.1 采用PCA 和t-SNE 维归约方法降维
分别采用PCA 和t-SNE 维归约方法将数据降维至64 维,并在低维空间重做相似性度量及其可视化操作。
> **维归约**的作用:
>
> - 避免维数灾难
> - 减少计算时间和存储消耗
> - 方便数据可视化
> - 减少不相关特征或噪声
#### 6.1.1 TCGA-BLCA
##### t-SNE方法
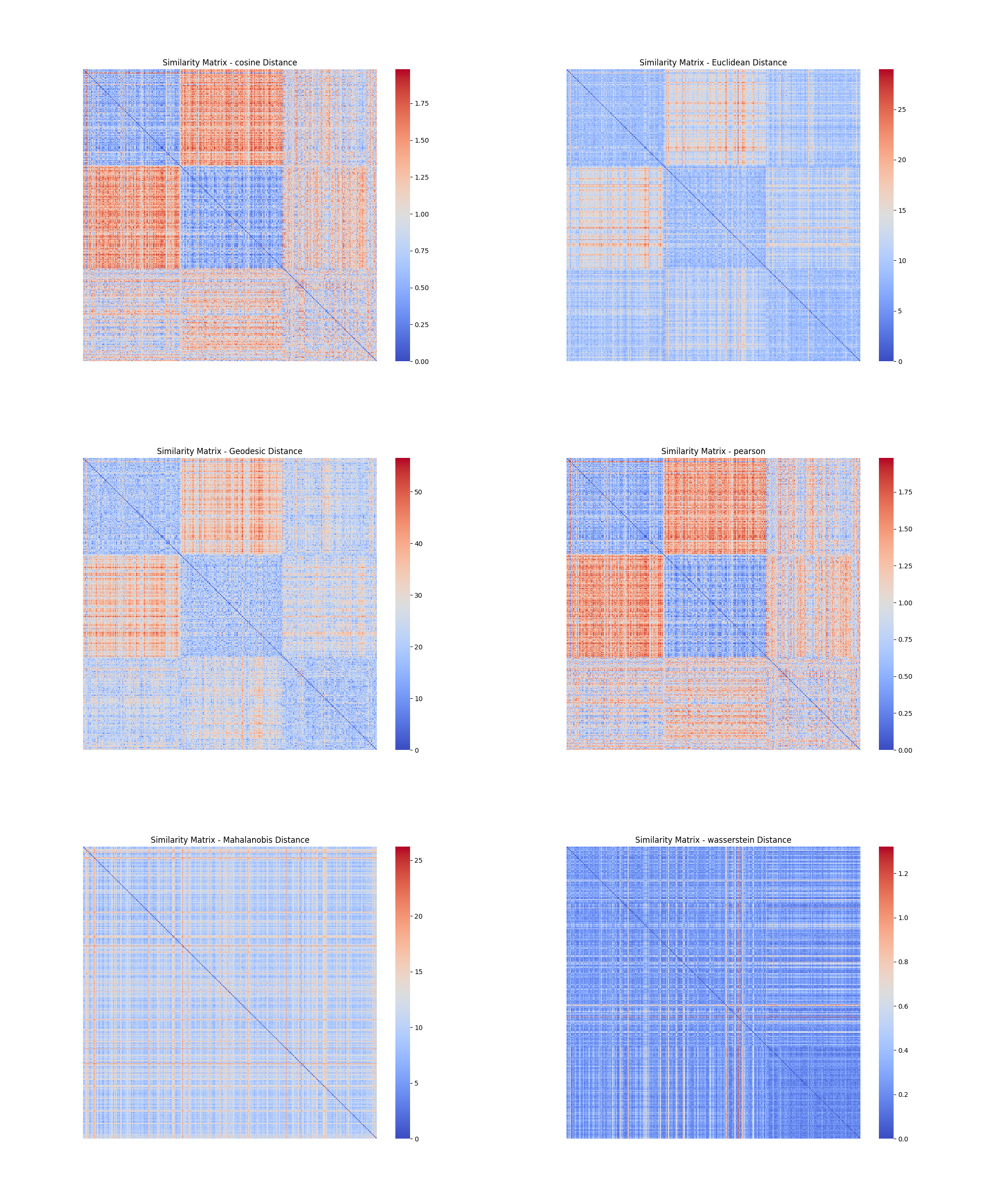
##### pca方法
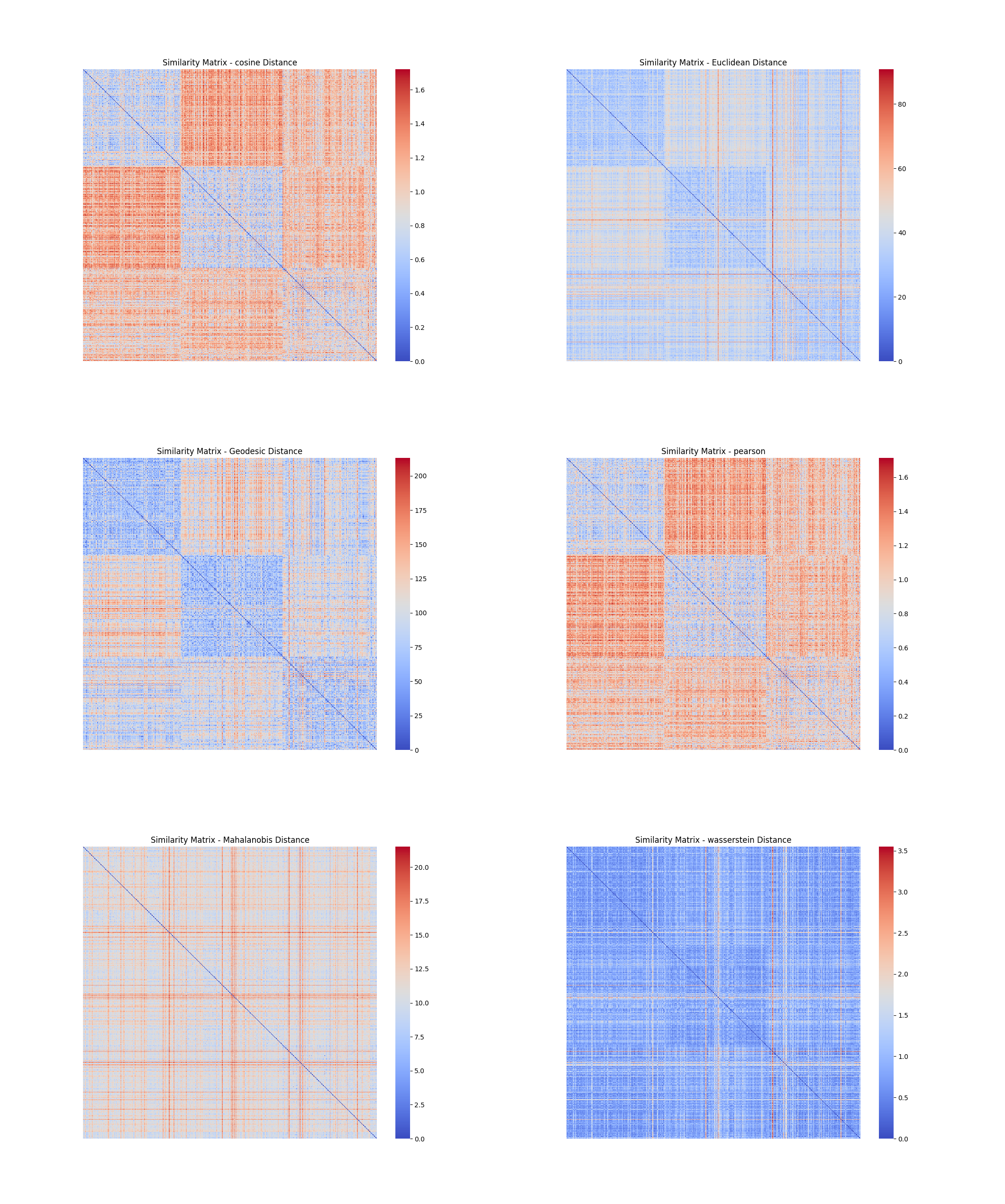
#### 6.1.2 TCGA-BRCA
##### t-SNE方法
.png)
##### pca方法
.png)
#### 6.1.3 TCGA-LGG
##### t-SNE方法
.png)
##### pca方法
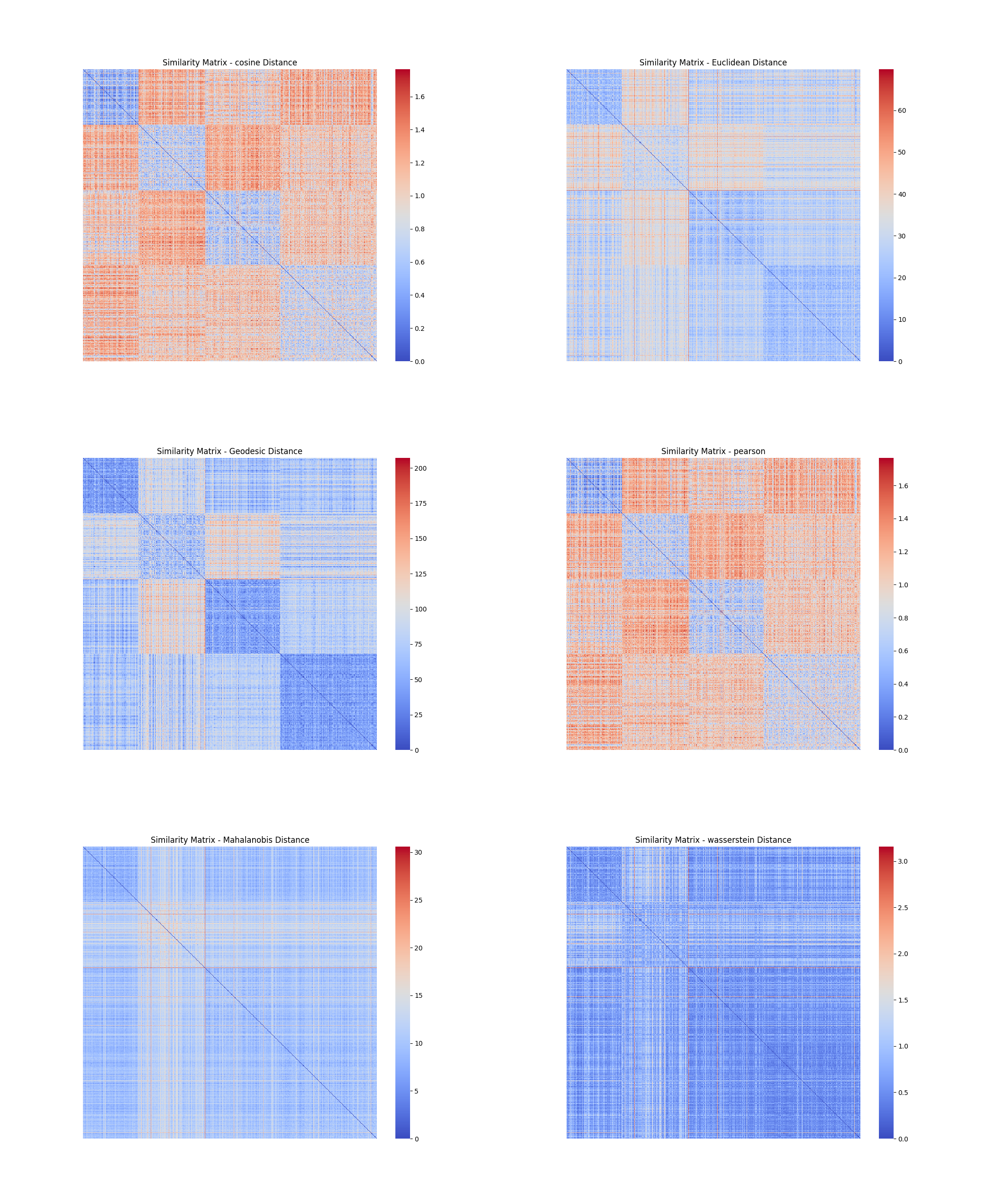
#### 6.1.4 TCGA-LUAD
##### t-SNE方法
.png)
##### pca方法
.png)
#### 6.1.5 TCGA-LUSC
##### t-SNE方法
.png)
##### pca方法
.png)
#### 6.1.6 分析
从以上各图,可以看到,经过降维以后,不仅**缓解了维度灾难,使得计算速度大大提升**(出图速度大大提示),且去除不相关或冗余特征,从而减少了噪声,使得数据更加清晰,**更容易看出数据的内在结构和模式**(图中明显分块,距离度量变得有意义)。在各个数据集上,可以看到,余弦距离和皮尔逊相关系数转化而来的距离效果比较好,测地距离也有不错的效果。
### 6.2 降维效果评估
取一个特定数据对象作为参考点,分别可视化维归约前后其它数据对象到该参考点的距离,观察比较 PCA 和 t-SNE 这两种降维方法**保持数据结构**的能力。
#### 6.2.1 TCGA-BLCA

#### 6.2.1 TCGA-BRCA
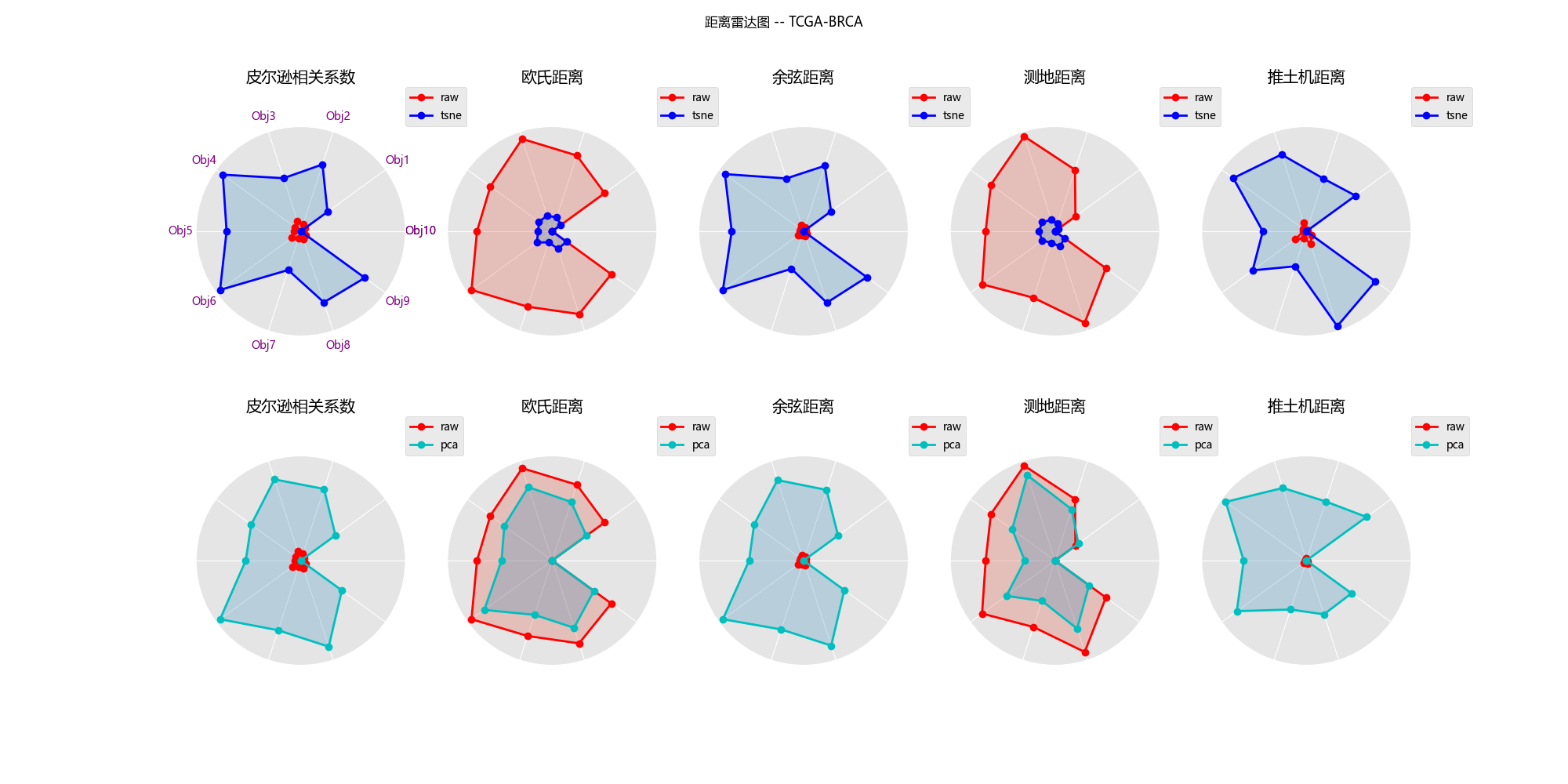
#### 6.2.3 TCGA-LGG
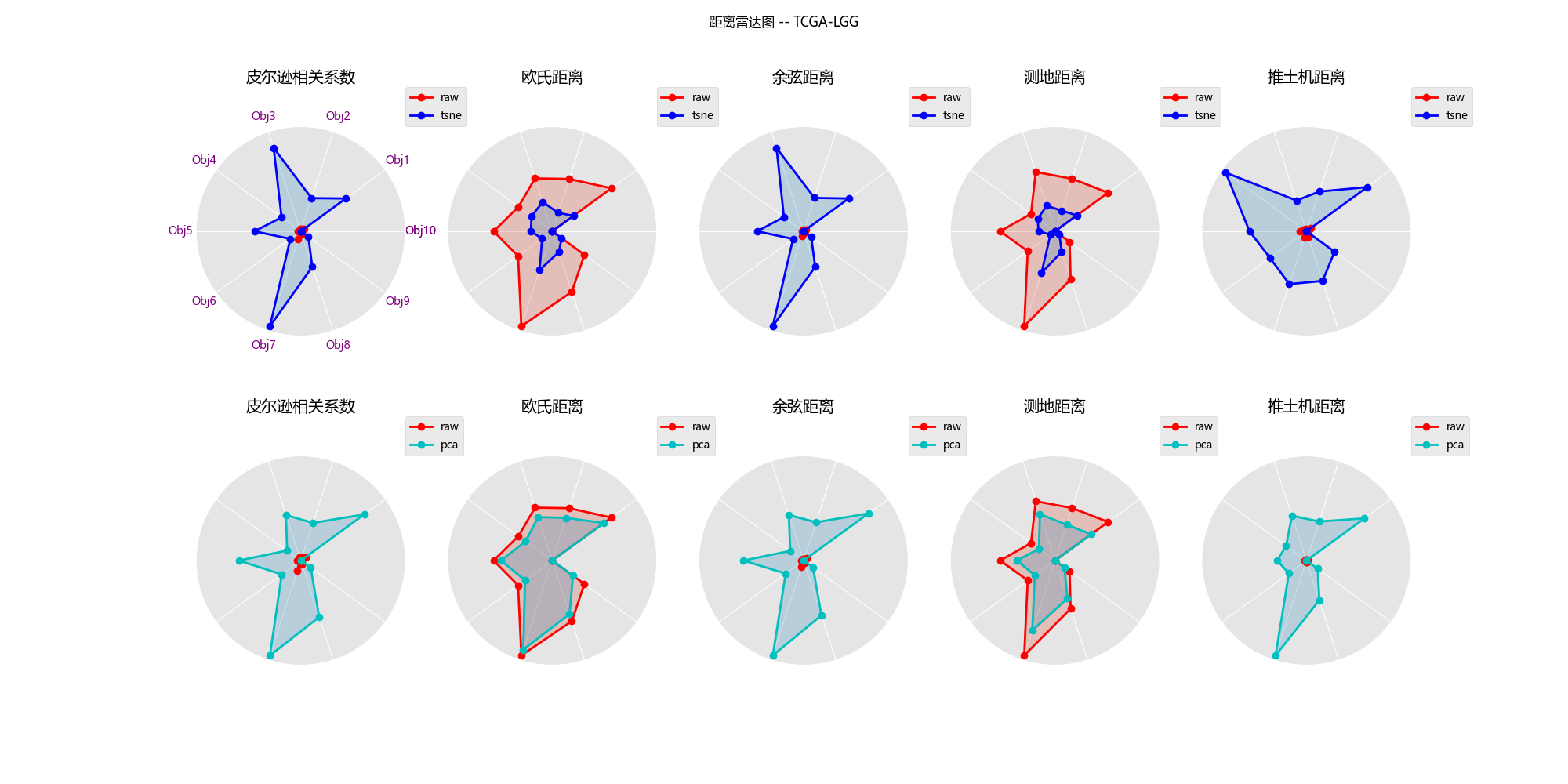
#### 6.2.4 TCGA-LUAD

#### 6.2.5 TCGA-LUSC
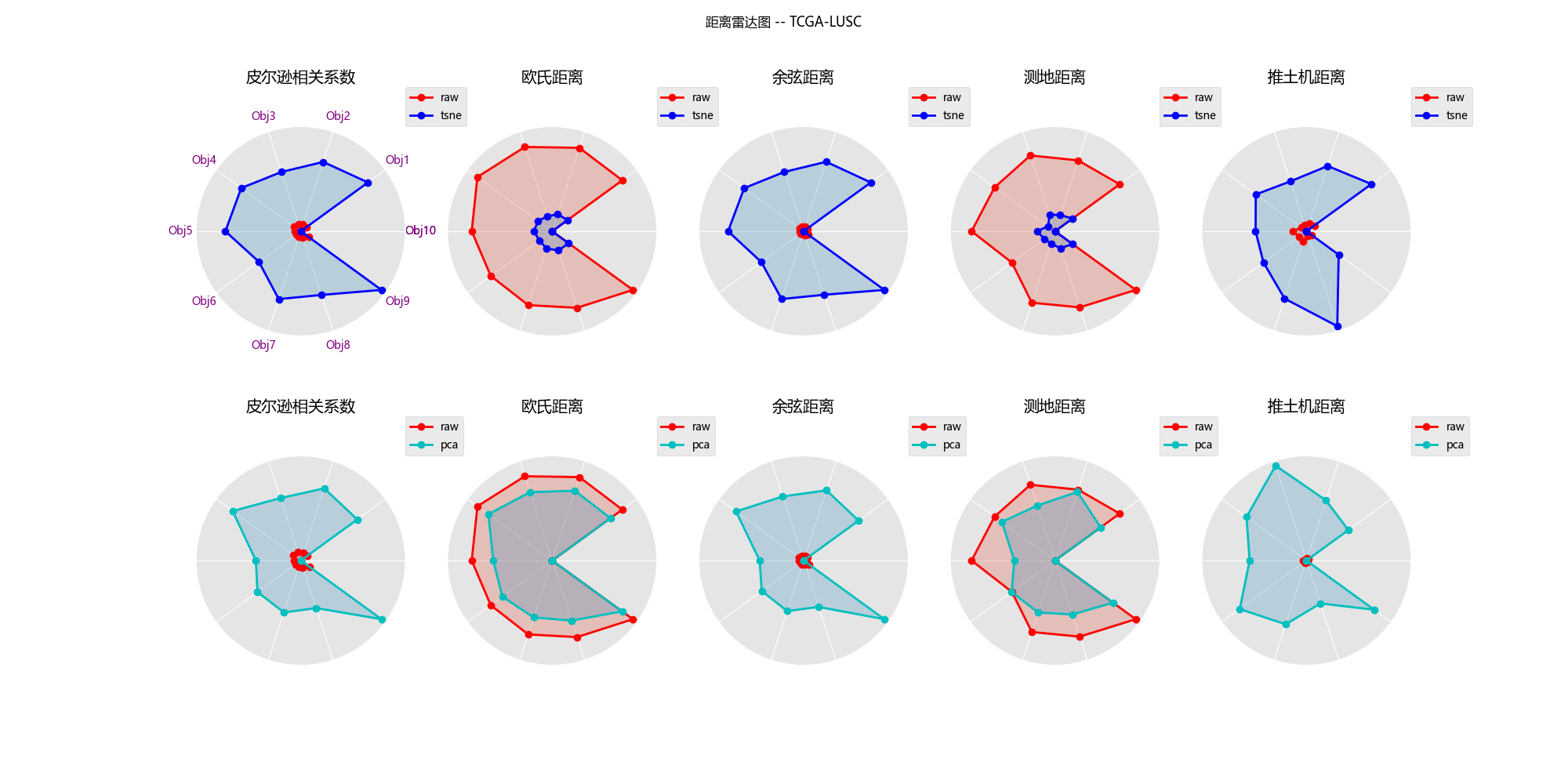
#### 6.2.6 分析
1. 线条形状越相似(另外十个数据对象到参考点的相对距离保持得越好),则降维效果越好(降维后数据结构保持得越好)
2. 尽管在五个数据集上两种降维方法对数据结构的保留能力各有优势,但总体而言,主成分分析法对欧式距离和测地距离度量具有较好的保持效果,而t-NSE在在这两种距离下保持数据结构的能力就不如pca方法,但t-NSE在推土机距离下仍能还原一定的数据结构,这是比pca方法好的
3. 而皮尔逊相关距离和余弦距离度量下,使用这两种降维方法效果都很差。
## 代码gitee地址
https://gitee.com/zhu-ronghui/data-mining.git
## 参考资料
1. t-SNE:最好的降维方法之一 - 马上科普的文章 - 知乎
https://zhuanlan.zhihu.com/p/64664346
2. Wattenberg, M., Viégas, F., & Johnson, I. (2016). How to Use t-SNE Effectively. Distill, 1(10), e2.(链接:https://distill.pub/2016/misread-tsne/)
3. [“维数灾难”怎么办?以医学癌症为例带你轻松化解 - 飞桨AI Studio星河社区 (baidu.com)](https://aistudio.baidu.com/projectdetail/3694652)
#### 4.2.6 分析
1. 直方图清晰地反映了该属性的表达值的分布情况,可以通过直方图的高度方便地看出数据的绝对频率(计数)或相对频率(概率密度)
2. 盒状图可以从宏观的角度看出属性的分布,并且直观明了地识别数据中的异常值(在上下限以外的菱形符号就表示异常值);并且盒状图突出显示了数据的**中位数**和**四分位数间距**,有助于了解数据的中心趋势。
3. 基因ENSG00000001460.18在TCGA-LGG这个类别的样本相较于其他四种癌症,表达量比较低,从直方图中可看出它在LGG数据集样本中表达量分布大致在0附近;观察盒状图可发现,该基因表达量中位数在LGG约为0.2,而在其他四个癌症中约为0.4,可以初步认为该基因在LGG数据集中相较于其他数据集不同。
### 4.3 采用t-SNE方法将数据集降维至2D 进行可视化。
1. 在之前的工作中,我们已经将各个数据集的样本数据聚集在.tsv文件中,因此我选择读取.tsv中的数据存取在pd.DataFrame中,并作转置,转置后的数据矩阵形状为(n_samples, n_rna_component)
2. 由于每个样本的RNA-seq的维度有大约30000,因此我选择使用t-sne对数据进行降维至2维进行可视化。
3. 在降维的过程中我们还可以根据各个数据集的sample type的不同,对不同的点进行不同染色,这样可以更方便地观察出不同类样本聚集成的簇的不同。我们可以借助DataFrame的索引来进行判断与过滤,得到样本的类别。
```python
#文件所属的病例的类型--sample type、
samplesheet_df[samplesheet_df['File Name'] == file.split('\\')[-1]]['Sample Type'].item()
```
4. 由于t-nse方法的学习率、困惑度(*perplexity*)都可能影响降维的效果。而根据文献推荐,困惑度的选择在5-50为佳,经过本人的实验,选择perplexity = 25或许会有比较好的效果。
以下便得到了,五个数据集的2D可视化图像(样本点颜色取决于样本类型):
#### 4.3.1 TCGA-BLCA

#### 4.3.2 TCGA-BRCA

#### 4.3.3 TCGA-LGG

#### 4.3.4 TCGA-LUAD

#### 4.3.5 TCGA-LUSC

#### 4.3.6 分析
通过可视化结果可以发现:
1. 除了在**BCLA**数据集中,Solid Tissue Normal——实体正常组织都能聚合在一个簇中,**并与癌症组织分开**。
2. Recurrent Tumor,复发型癌症的样本与原发癌症的样本常常混杂在一起,较难分开。
3. 尽管降维后的数据可视化图中的样本簇之间的距离并不能反映真实的样本距离,但可以认为癌症组织的RNA表达和正常组织的RNA表达确实存在差异,一定程度上可以被分隔开。
## 5. 相似性度量
分别采用:(a)欧式距离、(b)马氏距离(Mahalanobis distance)、(c)余弦距离、(d)Pearson 相关系数、(e)测地距离(geodesic distance)、(f)土机距离(Earth Mover's Distance, EMD)等6 种常见的距离(相似性)度量,计算数据对象之间的两两相似性,画出相似性矩阵(similarity matrix)。为了能反映出数据的内在模式,应先对数据进行初步聚类,将同簇的数据组织在一起。为此,可采用k-means 或其它方法在t-SNE 降维后的低维空间进行聚类。考虑做以下处理:
1. 使用t-SNE方法将五个数据集的数据矩阵降维到2维,并把数据矩阵储存在.tsv文件中
2. 利用k-means聚类算法对降低到2维的样本数据进行聚类,并根据聚类结果对数据集进行排序,使得同类数据聚集。
### 5.1 聚类与排序
在此之前我们先取k值为1~11,分别对五个数据集进行聚类,得到WCSS与K值的关系图,用于选取合适的k值。

选取好合适的k值后,我们把各自的k值存储在字典中,作为后面聚类的依据。聚类并排序完成后便可以计算相似度矩阵了。
### 5.2 原始数据的相似度矩阵
这里主要有2个点我没做好:
1. 这么大的数据矩阵,计算马氏距离和推土机距离距离的时间复杂度和空间复杂度都是很大的(尤其是马氏距离涉及到计算协方差矩阵,时间复杂度至少是n^2,对于高维情况下来说这是不敢想象的),因此在未降维的情况下,对于大数据集的数据矩阵比如BRCA的数据矩阵,高达(1200,30000),这样的数据量是**非常大**的。
2. 在计算各个数据集的马氏距离,我的笔电16G内存几乎跑满了也没法出图,经过实验计算到了后期性能瓶颈已经在于内存读取而不是cpu,几个小时不出图是很正常的。本人也查了些资料,也许可以利用Python的cudf利用gpu显存和cuda核心参与计算,可能有一定改善,但时间和技术所限,没有再试验下去了。
因此,下面的相似度矩阵将缺少部分的图。
#### 5.2.1 TCGA-BLCA

#### 5.2.2 TCGA-BRCA

#### 5.2.3 TCGA-LGG

#### 5.2.4 TCGA-LUAD

#### 5.2.5 TCGA-LUSC

#### 5.2.6 分析
从原始数据的相似度矩阵可以看出:
- 在高维情况下,余弦距离、欧式距离和皮尔逊相关距离区分不同簇的能力不强,不同分块之间的颜色有时几乎并无差别,都为蓝色。
- 距离矩阵容易被**个别样本或噪声**影响,导致距离的值变得极大,在热图上表现为鲜艳的红色。
## 6.维归约
### 6.1 采用PCA 和t-SNE 维归约方法降维
分别采用PCA 和t-SNE 维归约方法将数据降维至64 维,并在低维空间重做相似性度量及其可视化操作。
> **维归约**的作用:
>
> - 避免维数灾难
> - 减少计算时间和存储消耗
> - 方便数据可视化
> - 减少不相关特征或噪声
#### 6.1.1 TCGA-BLCA
##### t-SNE方法

##### pca方法

#### 6.1.2 TCGA-BRCA
##### t-SNE方法
.png)
##### pca方法
.png)
#### 6.1.3 TCGA-LGG
##### t-SNE方法
.png)
##### pca方法

#### 6.1.4 TCGA-LUAD
##### t-SNE方法
.png)
##### pca方法
.png)
#### 6.1.5 TCGA-LUSC
##### t-SNE方法
.png)
##### pca方法
.png)
#### 6.1.6 分析
从以上各图,可以看到,经过降维以后,不仅**缓解了维度灾难,使得计算速度大大提升**(出图速度大大提示),且去除不相关或冗余特征,从而减少了噪声,使得数据更加清晰,**更容易看出数据的内在结构和模式**(图中明显分块,距离度量变得有意义)。在各个数据集上,可以看到,余弦距离和皮尔逊相关系数转化而来的距离效果比较好,测地距离也有不错的效果。
### 6.2 降维效果评估
取一个特定数据对象作为参考点,分别可视化维归约前后其它数据对象到该参考点的距离,观察比较 PCA 和 t-SNE 这两种降维方法**保持数据结构**的能力。
#### 6.2.1 TCGA-BLCA

#### 6.2.1 TCGA-BRCA

#### 6.2.3 TCGA-LGG

#### 6.2.4 TCGA-LUAD

#### 6.2.5 TCGA-LUSC

#### 6.2.6 分析
1. 线条形状越相似(另外十个数据对象到参考点的相对距离保持得越好),则降维效果越好(降维后数据结构保持得越好)
2. 尽管在五个数据集上两种降维方法对数据结构的保留能力各有优势,但总体而言,主成分分析法对欧式距离和测地距离度量具有较好的保持效果,而t-NSE在在这两种距离下保持数据结构的能力就不如pca方法,但t-NSE在推土机距离下仍能还原一定的数据结构,这是比pca方法好的
3. 而皮尔逊相关距离和余弦距离度量下,使用这两种降维方法效果都很差。
## 代码gitee地址
https://gitee.com/zhu-ronghui/data-mining.git
## 参考资料
1. t-SNE:最好的降维方法之一 - 马上科普的文章 - 知乎
https://zhuanlan.zhihu.com/p/64664346
2. Wattenberg, M., Viégas, F., & Johnson, I. (2016). How to Use t-SNE Effectively. Distill, 1(10), e2.(链接:https://distill.pub/2016/misread-tsne/)
3. [“维数灾难”怎么办?以医学癌症为例带你轻松化解 - 飞桨AI Studio星河社区 (baidu.com)](https://aistudio.baidu.com/projectdetail/3694652) ## 3.数据处理
### 3.1 数据分类
在完成上一步的数据下载之后,我们会得到三千多个文件夹,这时候来自五个癌症的数据都是混杂在一起的,因此我们使用程序先把五种癌症的RNA数据分门别类的放好。在这里我选择了使用sample type对每种癌症的数据集进行分类,每种癌症都不太相同,但大致都有两类solid tissue normal(实体组织正常,也就是对照组)和Primary Tumor(原发性肿瘤)。
## 3.数据处理
### 3.1 数据分类
在完成上一步的数据下载之后,我们会得到三千多个文件夹,这时候来自五个癌症的数据都是混杂在一起的,因此我们使用程序先把五种癌症的RNA数据分门别类的放好。在这里我选择了使用sample type对每种癌症的数据集进行分类,每种癌症都不太相同,但大致都有两类solid tissue normal(实体组织正常,也就是对照组)和Primary Tumor(原发性肿瘤)。
 代码:
```python
import os
import shutil
# 定义文件夹路径
tcga_folder = 'TCGA' # 包含所有数据的文件夹
# 读取samplesheet.tsv文件
sample_sheet_path = 'gdc_sample_sheet.2024-04-07.tsv'
with open(sample_sheet_path, 'r') as file:
lines = file.readlines()
count =0
# 遍历
for line in lines:
count+=1
# 跳过标题行
if count==1:
continue
# 分割每一行的数据
parts = line.strip().split('\t')
file_id = parts[0] # 文件ID
project_id = parts[4] # 项目ID
sample_type = parts[7] # 样本类型
# 构建源文件夹路径
source_folder = os.path.join(tcga_folder, file_id)
# 构建目标文件夹路径
target_folder = os.path.join(project_id, sample_type)
os.makedirs(target_folder, exist_ok=True) # 确保目标文件夹存在
# 移动文件夹
shutil.move(source_folder, target_folder)
print(f'Moved {source_folder} to {target_folder}')
print(count)
```
### 3.2 数据预处理(聚集、清洗、标准化)
1. 观察原始数据的可发现第一列为gene_id,最后一列为fpkm_uq_unstranded(未校正的每千个碱基的片段数),且前四行都是表达量的统计信息,因此第四行以后是我们需要使用的数据。
2. 由于此时每个癌症样本的RNA数据独立存在于.tsv文件中,不利于后续处理。因此我们需要提取每个RNA-seq文件的最后一列(前四行不包括),并把它们拼接起来,形成一个数据矩阵,完成**数据聚集**。
3. 观察原始数据可知,有大量基因表达量为0,因此选择做**数据清洗**:对于每一个数据集,在 6 万多个 RNA 中,如果某RNA在一半以上的病例中没有表达(数值为0),则将其丢弃(最终剩余3 万个左右的基因用于分析)
4. 对于完成前面处理的数据而已,我们还要做数据标准化$x = log_{10}(x + 1)$,这样可以保证各个数据大致在一个数量级,方便后续的处理。
使用一个函数来完成上述过程,并把结果存储在.tsv文件中,方便后续调用:
```python
def pre_process(file_dir):
temp_df = pd.DataFrame()
cases = find_cases(file_dir)
for i, case in enumerate(tqdm(cases)):
df_test = pd.read_csv(case[0],sep='\t',comment='#',header=0,index_col=0)
temp_df = pd.concat([temp_df,df_test.iloc[4:,7]],axis=1,ignore_index=False)
# temp_df = temp_df.transpose()
print(temp_df,temp_df.shape)
# return
index_list = []
for i in range(temp_df.shape[0]):
number = dict(temp_df.iloc[i].value_counts(normalize=True)) # 统计第i行所有元素的个数(以百分比形式显示)
number_default_value = defaultdict(int,number) # 为防止字典里没有KEY0.0,从而使用defaultdict
if number_default_value[0.0] > 0.5: # 如果某RNA在一半以上的病例中没有表达(数值为0),则将其丢弃
index_list.append(i) # 将对应的行号放入列表中
# 删除指定行(index_list里的行数)
temp_df = temp_df.drop(temp_df.index[index_list])
temp_df = temp_df.apply(lambda x : np.log10(x+1)) #对数标准化
new_column_names = [str(i) for i in range(temp_df.shape[1])]
temp_df.columns = new_column_names
print(temp_df,temp_df.shape)
temp_df.to_csv(f'{file_dir}.tsv',sep='\t')
return
```
## 4.数据的初步探索和可视化
### 4.1 分别画出五个数据集的的数据矩阵图(data matrix)
> 数据集的数据矩阵图(也称为热图或矩阵图)是一种可视化工具,用于展示数据集中多个变量之间的关系,或者展示数据集中多个样本之间的相似性和差异性。在这种图表中,数据被组织成一个矩阵的形式,矩阵中的每个单元格代表一个变量(或样本)与另一个变量(或样本)之间的关系或比较。
以下分别为TCGA-BLCA, TCGA-BRCA, TCGA-LGG, TCGA-LUAD 和TCGA-LUSC数据集的数据矩阵图。
#### 4.1.1 TCGA-BLCA
代码:
```python
import os
import shutil
# 定义文件夹路径
tcga_folder = 'TCGA' # 包含所有数据的文件夹
# 读取samplesheet.tsv文件
sample_sheet_path = 'gdc_sample_sheet.2024-04-07.tsv'
with open(sample_sheet_path, 'r') as file:
lines = file.readlines()
count =0
# 遍历
for line in lines:
count+=1
# 跳过标题行
if count==1:
continue
# 分割每一行的数据
parts = line.strip().split('\t')
file_id = parts[0] # 文件ID
project_id = parts[4] # 项目ID
sample_type = parts[7] # 样本类型
# 构建源文件夹路径
source_folder = os.path.join(tcga_folder, file_id)
# 构建目标文件夹路径
target_folder = os.path.join(project_id, sample_type)
os.makedirs(target_folder, exist_ok=True) # 确保目标文件夹存在
# 移动文件夹
shutil.move(source_folder, target_folder)
print(f'Moved {source_folder} to {target_folder}')
print(count)
```
### 3.2 数据预处理(聚集、清洗、标准化)
1. 观察原始数据的可发现第一列为gene_id,最后一列为fpkm_uq_unstranded(未校正的每千个碱基的片段数),且前四行都是表达量的统计信息,因此第四行以后是我们需要使用的数据。
2. 由于此时每个癌症样本的RNA数据独立存在于.tsv文件中,不利于后续处理。因此我们需要提取每个RNA-seq文件的最后一列(前四行不包括),并把它们拼接起来,形成一个数据矩阵,完成**数据聚集**。
3. 观察原始数据可知,有大量基因表达量为0,因此选择做**数据清洗**:对于每一个数据集,在 6 万多个 RNA 中,如果某RNA在一半以上的病例中没有表达(数值为0),则将其丢弃(最终剩余3 万个左右的基因用于分析)
4. 对于完成前面处理的数据而已,我们还要做数据标准化$x = log_{10}(x + 1)$,这样可以保证各个数据大致在一个数量级,方便后续的处理。
使用一个函数来完成上述过程,并把结果存储在.tsv文件中,方便后续调用:
```python
def pre_process(file_dir):
temp_df = pd.DataFrame()
cases = find_cases(file_dir)
for i, case in enumerate(tqdm(cases)):
df_test = pd.read_csv(case[0],sep='\t',comment='#',header=0,index_col=0)
temp_df = pd.concat([temp_df,df_test.iloc[4:,7]],axis=1,ignore_index=False)
# temp_df = temp_df.transpose()
print(temp_df,temp_df.shape)
# return
index_list = []
for i in range(temp_df.shape[0]):
number = dict(temp_df.iloc[i].value_counts(normalize=True)) # 统计第i行所有元素的个数(以百分比形式显示)
number_default_value = defaultdict(int,number) # 为防止字典里没有KEY0.0,从而使用defaultdict
if number_default_value[0.0] > 0.5: # 如果某RNA在一半以上的病例中没有表达(数值为0),则将其丢弃
index_list.append(i) # 将对应的行号放入列表中
# 删除指定行(index_list里的行数)
temp_df = temp_df.drop(temp_df.index[index_list])
temp_df = temp_df.apply(lambda x : np.log10(x+1)) #对数标准化
new_column_names = [str(i) for i in range(temp_df.shape[1])]
temp_df.columns = new_column_names
print(temp_df,temp_df.shape)
temp_df.to_csv(f'{file_dir}.tsv',sep='\t')
return
```
## 4.数据的初步探索和可视化
### 4.1 分别画出五个数据集的的数据矩阵图(data matrix)
> 数据集的数据矩阵图(也称为热图或矩阵图)是一种可视化工具,用于展示数据集中多个变量之间的关系,或者展示数据集中多个样本之间的相似性和差异性。在这种图表中,数据被组织成一个矩阵的形式,矩阵中的每个单元格代表一个变量(或样本)与另一个变量(或样本)之间的关系或比较。
以下分别为TCGA-BLCA, TCGA-BRCA, TCGA-LGG, TCGA-LUAD 和TCGA-LUSC数据集的数据矩阵图。
#### 4.1.1 TCGA-BLCA
 #### 4.1.2 TCGA-BRCA
#### 4.1.2 TCGA-BRCA
 #### 4.1.3 TCGA-LGG
#### 4.1.3 TCGA-LGG
 #### 4.1.4 TCGA-LUAD
#### 4.1.4 TCGA-LUAD
 #### 4.1.5 TCGA-LUSC
#### 4.1.5 TCGA-LUSC
 ### 4.2 任选10 个RNA 维度(属性),分别画出每个维度的直方图和盒状图,并进行跨数据集比较。
经过观察我发现,基因ID为:ENSG00000000419.13、ENSG00000000457.14、ENSG00000000460.17、ENSG00000000938.13、ENSG00000000971.16、ENSG00000001036.14、ENSG00000001084.13、ENSG00000001167.14、ENSG00000001460.18和ENSG00000001461.17的基因在五种癌症中都有较高的表达了,不妨选取这十个RNA维度并绘制相关图像进行比较分析。
#### 4.2.1 TCGA-BLCA
### 4.2 任选10 个RNA 维度(属性),分别画出每个维度的直方图和盒状图,并进行跨数据集比较。
经过观察我发现,基因ID为:ENSG00000000419.13、ENSG00000000457.14、ENSG00000000460.17、ENSG00000000938.13、ENSG00000000971.16、ENSG00000001036.14、ENSG00000001084.13、ENSG00000001167.14、ENSG00000001460.18和ENSG00000001461.17的基因在五种癌症中都有较高的表达了,不妨选取这十个RNA维度并绘制相关图像进行比较分析。
#### 4.2.1 TCGA-BLCA
 #### 4.2.2 TCGA-BRCA
#### 4.2.2 TCGA-BRCA
 #### 4.2.3 TCGA-LGG
#### 4.2.3 TCGA-LGG
 #### 4.2.4 TCGA-LUAD
#### 4.2.4 TCGA-LUAD
 #### 4.2.5 TCGA-LUSC
#### 4.2.5 TCGA-LUSC
 #### 4.2.6 分析
1. 直方图清晰地反映了该属性的表达值的分布情况,可以通过直方图的高度方便地看出数据的绝对频率(计数)或相对频率(概率密度)
2. 盒状图可以从宏观的角度看出属性的分布,并且直观明了地识别数据中的异常值(在上下限以外的菱形符号就表示异常值);并且盒状图突出显示了数据的**中位数**和**四分位数间距**,有助于了解数据的中心趋势。
3. 基因ENSG00000001460.18在TCGA-LGG这个类别的样本相较于其他四种癌症,表达量比较低,从直方图中可看出它在LGG数据集样本中表达量分布大致在0附近;观察盒状图可发现,该基因表达量中位数在LGG约为0.2,而在其他四个癌症中约为0.4,可以初步认为该基因在LGG数据集中相较于其他数据集不同。
### 4.3 采用t-SNE方法将数据集降维至2D 进行可视化。
1. 在之前的工作中,我们已经将各个数据集的样本数据聚集在.tsv文件中,因此我选择读取.tsv中的数据存取在pd.DataFrame中,并作转置,转置后的数据矩阵形状为(n_samples, n_rna_component)
2. 由于每个样本的RNA-seq的维度有大约30000,因此我选择使用t-sne对数据进行降维至2维进行可视化。
3. 在降维的过程中我们还可以根据各个数据集的sample type的不同,对不同的点进行不同染色,这样可以更方便地观察出不同类样本聚集成的簇的不同。我们可以借助DataFrame的索引来进行判断与过滤,得到样本的类别。
```python
#文件所属的病例的类型--sample type、
samplesheet_df[samplesheet_df['File Name'] == file.split('\\')[-1]]['Sample Type'].item()
```
4. 由于t-nse方法的学习率、困惑度(*perplexity*)都可能影响降维的效果。而根据文献推荐,困惑度的选择在5-50为佳,经过本人的实验,选择perplexity = 25或许会有比较好的效果。
以下便得到了,五个数据集的2D可视化图像(样本点颜色取决于样本类型):
#### 4.3.1 TCGA-BLCA

#### 4.3.2 TCGA-BRCA

#### 4.3.3 TCGA-LGG

#### 4.3.4 TCGA-LUAD

#### 4.3.5 TCGA-LUSC

#### 4.3.6 分析
通过可视化结果可以发现:
1. 除了在**BCLA**数据集中,Solid Tissue Normal——实体正常组织都能聚合在一个簇中,**并与癌症组织分开**。
2. Recurrent Tumor,复发型癌症的样本与原发癌症的样本常常混杂在一起,较难分开。
3. 尽管降维后的数据可视化图中的样本簇之间的距离并不能反映真实的样本距离,但可以认为癌症组织的RNA表达和正常组织的RNA表达确实存在差异,一定程度上可以被分隔开。
## 5. 相似性度量
分别采用:(a)欧式距离、(b)马氏距离(Mahalanobis distance)、(c)余弦距离、(d)Pearson 相关系数、(e)测地距离(geodesic distance)、(f)土机距离(Earth Mover's Distance, EMD)等6 种常见的距离(相似性)度量,计算数据对象之间的两两相似性,画出相似性矩阵(similarity matrix)。为了能反映出数据的内在模式,应先对数据进行初步聚类,将同簇的数据组织在一起。为此,可采用k-means 或其它方法在t-SNE 降维后的低维空间进行聚类。考虑做以下处理:
1. 使用t-SNE方法将五个数据集的数据矩阵降维到2维,并把数据矩阵储存在.tsv文件中
2. 利用k-means聚类算法对降低到2维的样本数据进行聚类,并根据聚类结果对数据集进行排序,使得同类数据聚集。
### 5.1 聚类与排序
在此之前我们先取k值为1~11,分别对五个数据集进行聚类,得到WCSS与K值的关系图,用于选取合适的k值。

选取好合适的k值后,我们把各自的k值存储在字典中,作为后面聚类的依据。聚类并排序完成后便可以计算相似度矩阵了。
### 5.2 原始数据的相似度矩阵
这里主要有2个点我没做好:
1. 这么大的数据矩阵,计算马氏距离和推土机距离距离的时间复杂度和空间复杂度都是很大的(尤其是马氏距离涉及到计算协方差矩阵,时间复杂度至少是n^2,对于高维情况下来说这是不敢想象的),因此在未降维的情况下,对于大数据集的数据矩阵比如BRCA的数据矩阵,高达(1200,30000),这样的数据量是**非常大**的。
2. 在计算各个数据集的马氏距离,我的笔电16G内存几乎跑满了也没法出图,经过实验计算到了后期性能瓶颈已经在于内存读取而不是cpu,几个小时不出图是很正常的。本人也查了些资料,也许可以利用Python的cudf利用gpu显存和cuda核心参与计算,可能有一定改善,但时间和技术所限,没有再试验下去了。
因此,下面的相似度矩阵将缺少部分的图。
#### 5.2.1 TCGA-BLCA

#### 5.2.2 TCGA-BRCA

#### 5.2.3 TCGA-LGG

#### 5.2.4 TCGA-LUAD

#### 5.2.5 TCGA-LUSC

#### 5.2.6 分析
从原始数据的相似度矩阵可以看出:
- 在高维情况下,余弦距离、欧式距离和皮尔逊相关距离区分不同簇的能力不强,不同分块之间的颜色有时几乎并无差别,都为蓝色。
- 距离矩阵容易被**个别样本或噪声**影响,导致距离的值变得极大,在热图上表现为鲜艳的红色。
## 6.维归约
### 6.1 采用PCA 和t-SNE 维归约方法降维
分别采用PCA 和t-SNE 维归约方法将数据降维至64 维,并在低维空间重做相似性度量及其可视化操作。
> **维归约**的作用:
>
> - 避免维数灾难
> - 减少计算时间和存储消耗
> - 方便数据可视化
> - 减少不相关特征或噪声
#### 6.1.1 TCGA-BLCA
##### t-SNE方法

##### pca方法

#### 6.1.2 TCGA-BRCA
##### t-SNE方法
.png)
##### pca方法
.png)
#### 6.1.3 TCGA-LGG
##### t-SNE方法
.png)
##### pca方法

#### 6.1.4 TCGA-LUAD
##### t-SNE方法
.png)
##### pca方法
.png)
#### 6.1.5 TCGA-LUSC
##### t-SNE方法
.png)
##### pca方法
.png)
#### 6.1.6 分析
从以上各图,可以看到,经过降维以后,不仅**缓解了维度灾难,使得计算速度大大提升**(出图速度大大提示),且去除不相关或冗余特征,从而减少了噪声,使得数据更加清晰,**更容易看出数据的内在结构和模式**(图中明显分块,距离度量变得有意义)。在各个数据集上,可以看到,余弦距离和皮尔逊相关系数转化而来的距离效果比较好,测地距离也有不错的效果。
### 6.2 降维效果评估
取一个特定数据对象作为参考点,分别可视化维归约前后其它数据对象到该参考点的距离,观察比较 PCA 和 t-SNE 这两种降维方法**保持数据结构**的能力。
#### 6.2.1 TCGA-BLCA

#### 6.2.1 TCGA-BRCA

#### 6.2.3 TCGA-LGG

#### 6.2.4 TCGA-LUAD

#### 6.2.5 TCGA-LUSC

#### 6.2.6 分析
1. 线条形状越相似(另外十个数据对象到参考点的相对距离保持得越好),则降维效果越好(降维后数据结构保持得越好)
2. 尽管在五个数据集上两种降维方法对数据结构的保留能力各有优势,但总体而言,主成分分析法对欧式距离和测地距离度量具有较好的保持效果,而t-NSE在在这两种距离下保持数据结构的能力就不如pca方法,但t-NSE在推土机距离下仍能还原一定的数据结构,这是比pca方法好的
3. 而皮尔逊相关距离和余弦距离度量下,使用这两种降维方法效果都很差。
## 代码gitee地址
https://gitee.com/zhu-ronghui/data-mining.git
## 参考资料
1. t-SNE:最好的降维方法之一 - 马上科普的文章 - 知乎
https://zhuanlan.zhihu.com/p/64664346
2. Wattenberg, M., Viégas, F., & Johnson, I. (2016). How to Use t-SNE Effectively. Distill, 1(10), e2.(链接:https://distill.pub/2016/misread-tsne/)
3. [“维数灾难”怎么办?以医学癌症为例带你轻松化解 - 飞桨AI Studio星河社区 (baidu.com)](https://aistudio.baidu.com/projectdetail/3694652)
#### 4.2.6 分析
1. 直方图清晰地反映了该属性的表达值的分布情况,可以通过直方图的高度方便地看出数据的绝对频率(计数)或相对频率(概率密度)
2. 盒状图可以从宏观的角度看出属性的分布,并且直观明了地识别数据中的异常值(在上下限以外的菱形符号就表示异常值);并且盒状图突出显示了数据的**中位数**和**四分位数间距**,有助于了解数据的中心趋势。
3. 基因ENSG00000001460.18在TCGA-LGG这个类别的样本相较于其他四种癌症,表达量比较低,从直方图中可看出它在LGG数据集样本中表达量分布大致在0附近;观察盒状图可发现,该基因表达量中位数在LGG约为0.2,而在其他四个癌症中约为0.4,可以初步认为该基因在LGG数据集中相较于其他数据集不同。
### 4.3 采用t-SNE方法将数据集降维至2D 进行可视化。
1. 在之前的工作中,我们已经将各个数据集的样本数据聚集在.tsv文件中,因此我选择读取.tsv中的数据存取在pd.DataFrame中,并作转置,转置后的数据矩阵形状为(n_samples, n_rna_component)
2. 由于每个样本的RNA-seq的维度有大约30000,因此我选择使用t-sne对数据进行降维至2维进行可视化。
3. 在降维的过程中我们还可以根据各个数据集的sample type的不同,对不同的点进行不同染色,这样可以更方便地观察出不同类样本聚集成的簇的不同。我们可以借助DataFrame的索引来进行判断与过滤,得到样本的类别。
```python
#文件所属的病例的类型--sample type、
samplesheet_df[samplesheet_df['File Name'] == file.split('\\')[-1]]['Sample Type'].item()
```
4. 由于t-nse方法的学习率、困惑度(*perplexity*)都可能影响降维的效果。而根据文献推荐,困惑度的选择在5-50为佳,经过本人的实验,选择perplexity = 25或许会有比较好的效果。
以下便得到了,五个数据集的2D可视化图像(样本点颜色取决于样本类型):
#### 4.3.1 TCGA-BLCA

#### 4.3.2 TCGA-BRCA

#### 4.3.3 TCGA-LGG

#### 4.3.4 TCGA-LUAD

#### 4.3.5 TCGA-LUSC

#### 4.3.6 分析
通过可视化结果可以发现:
1. 除了在**BCLA**数据集中,Solid Tissue Normal——实体正常组织都能聚合在一个簇中,**并与癌症组织分开**。
2. Recurrent Tumor,复发型癌症的样本与原发癌症的样本常常混杂在一起,较难分开。
3. 尽管降维后的数据可视化图中的样本簇之间的距离并不能反映真实的样本距离,但可以认为癌症组织的RNA表达和正常组织的RNA表达确实存在差异,一定程度上可以被分隔开。
## 5. 相似性度量
分别采用:(a)欧式距离、(b)马氏距离(Mahalanobis distance)、(c)余弦距离、(d)Pearson 相关系数、(e)测地距离(geodesic distance)、(f)土机距离(Earth Mover's Distance, EMD)等6 种常见的距离(相似性)度量,计算数据对象之间的两两相似性,画出相似性矩阵(similarity matrix)。为了能反映出数据的内在模式,应先对数据进行初步聚类,将同簇的数据组织在一起。为此,可采用k-means 或其它方法在t-SNE 降维后的低维空间进行聚类。考虑做以下处理:
1. 使用t-SNE方法将五个数据集的数据矩阵降维到2维,并把数据矩阵储存在.tsv文件中
2. 利用k-means聚类算法对降低到2维的样本数据进行聚类,并根据聚类结果对数据集进行排序,使得同类数据聚集。
### 5.1 聚类与排序
在此之前我们先取k值为1~11,分别对五个数据集进行聚类,得到WCSS与K值的关系图,用于选取合适的k值。

选取好合适的k值后,我们把各自的k值存储在字典中,作为后面聚类的依据。聚类并排序完成后便可以计算相似度矩阵了。
### 5.2 原始数据的相似度矩阵
这里主要有2个点我没做好:
1. 这么大的数据矩阵,计算马氏距离和推土机距离距离的时间复杂度和空间复杂度都是很大的(尤其是马氏距离涉及到计算协方差矩阵,时间复杂度至少是n^2,对于高维情况下来说这是不敢想象的),因此在未降维的情况下,对于大数据集的数据矩阵比如BRCA的数据矩阵,高达(1200,30000),这样的数据量是**非常大**的。
2. 在计算各个数据集的马氏距离,我的笔电16G内存几乎跑满了也没法出图,经过实验计算到了后期性能瓶颈已经在于内存读取而不是cpu,几个小时不出图是很正常的。本人也查了些资料,也许可以利用Python的cudf利用gpu显存和cuda核心参与计算,可能有一定改善,但时间和技术所限,没有再试验下去了。
因此,下面的相似度矩阵将缺少部分的图。
#### 5.2.1 TCGA-BLCA

#### 5.2.2 TCGA-BRCA

#### 5.2.3 TCGA-LGG

#### 5.2.4 TCGA-LUAD

#### 5.2.5 TCGA-LUSC

#### 5.2.6 分析
从原始数据的相似度矩阵可以看出:
- 在高维情况下,余弦距离、欧式距离和皮尔逊相关距离区分不同簇的能力不强,不同分块之间的颜色有时几乎并无差别,都为蓝色。
- 距离矩阵容易被**个别样本或噪声**影响,导致距离的值变得极大,在热图上表现为鲜艳的红色。
## 6.维归约
### 6.1 采用PCA 和t-SNE 维归约方法降维
分别采用PCA 和t-SNE 维归约方法将数据降维至64 维,并在低维空间重做相似性度量及其可视化操作。
> **维归约**的作用:
>
> - 避免维数灾难
> - 减少计算时间和存储消耗
> - 方便数据可视化
> - 减少不相关特征或噪声
#### 6.1.1 TCGA-BLCA
##### t-SNE方法

##### pca方法

#### 6.1.2 TCGA-BRCA
##### t-SNE方法
.png)
##### pca方法
.png)
#### 6.1.3 TCGA-LGG
##### t-SNE方法
.png)
##### pca方法

#### 6.1.4 TCGA-LUAD
##### t-SNE方法
.png)
##### pca方法
.png)
#### 6.1.5 TCGA-LUSC
##### t-SNE方法
.png)
##### pca方法
.png)
#### 6.1.6 分析
从以上各图,可以看到,经过降维以后,不仅**缓解了维度灾难,使得计算速度大大提升**(出图速度大大提示),且去除不相关或冗余特征,从而减少了噪声,使得数据更加清晰,**更容易看出数据的内在结构和模式**(图中明显分块,距离度量变得有意义)。在各个数据集上,可以看到,余弦距离和皮尔逊相关系数转化而来的距离效果比较好,测地距离也有不错的效果。
### 6.2 降维效果评估
取一个特定数据对象作为参考点,分别可视化维归约前后其它数据对象到该参考点的距离,观察比较 PCA 和 t-SNE 这两种降维方法**保持数据结构**的能力。
#### 6.2.1 TCGA-BLCA

#### 6.2.1 TCGA-BRCA

#### 6.2.3 TCGA-LGG

#### 6.2.4 TCGA-LUAD

#### 6.2.5 TCGA-LUSC

#### 6.2.6 分析
1. 线条形状越相似(另外十个数据对象到参考点的相对距离保持得越好),则降维效果越好(降维后数据结构保持得越好)
2. 尽管在五个数据集上两种降维方法对数据结构的保留能力各有优势,但总体而言,主成分分析法对欧式距离和测地距离度量具有较好的保持效果,而t-NSE在在这两种距离下保持数据结构的能力就不如pca方法,但t-NSE在推土机距离下仍能还原一定的数据结构,这是比pca方法好的
3. 而皮尔逊相关距离和余弦距离度量下,使用这两种降维方法效果都很差。
## 代码gitee地址
https://gitee.com/zhu-ronghui/data-mining.git
## 参考资料
1. t-SNE:最好的降维方法之一 - 马上科普的文章 - 知乎
https://zhuanlan.zhihu.com/p/64664346
2. Wattenberg, M., Viégas, F., & Johnson, I. (2016). How to Use t-SNE Effectively. Distill, 1(10), e2.(链接:https://distill.pub/2016/misread-tsne/)
3. [“维数灾难”怎么办?以医学癌症为例带你轻松化解 - 飞桨AI Studio星河社区 (baidu.com)](https://aistudio.baidu.com/projectdetail/3694652)