堆栈(Stack):简称为栈。一种线性表数据结构,是一种只允许在表的一端进行插入和删除操作的线性表。
我们把栈中允许插入和删除的一端称为 「栈顶(top)」;另一端则称为 「栈底(bottom)」。当表中没有任何数据元素时,称之为 「空栈」。
堆栈有两种基本操作:「插入操作」 和 「删除操作」。
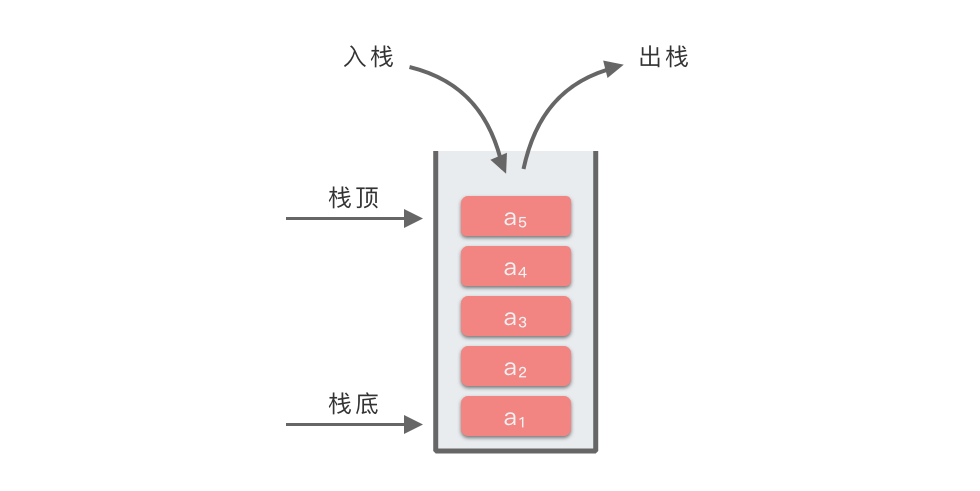
简单来说,栈是一种 「后进先出(Last In First Out)」 的线性表,简称为 「LIFO 结构」。
我们可以从两个方面来解释一下栈的定义:
栈首先是一个线性表,栈中元素具有前驱后继的线性关系。栈中元素按照 $a_1, a_2, ... , a_n$ 的次序依次进栈。栈顶元素为 $a_n$。
根据堆栈的定义,每次删除的总是堆栈中当前的栈顶元素,即最后进入堆栈的元素。而在进栈时,最先进入堆栈的元素一定在栈底,最后进入堆栈的元素一定在栈顶。也就是说,元素进入堆栈或者退出退栈是按照「后进先出(Last In First Out)」的原则进行的。
和线性表类似,栈有两种存储表示方法:「顺序栈」 和 「链式栈」。
在描述堆栈的顺序存储与链式存储具体实现之前,我们先来看看堆栈具有哪些基本操作。
栈作为一种线性表来说,理论上应该具备线性表所有的操作特性,但由于「后进先出」的特殊性,所以针对栈的操作进行了一些变化。尤其是插入操作和删除操作,改为了入栈(push)和出栈(pop)。
堆栈的基本操作如下:
初始化空栈:创建一个空栈,定义栈的大小 $size$,以及栈顶元素指针 $top$。
判断栈是否为空:当堆栈为空时,返回 $True$。当堆栈不为空时,返回 $False$。一般只用于栈中删除操作和获取当前栈顶元素操作中。
判断栈是否已满:当堆栈已满时,返回 $True$,当堆栈未满时,返回 $False$。一般只用于顺序栈中插入元素和获取当前栈顶元素操作中。
插入元素(进栈、入栈):相当于在线性表最后元素后面插入一个新的数据元素。并改变栈顶指针 $top$ 的指向位置。
删除元素(出栈、退栈):相当于在线性表最后元素后面删除最后一个数据元素。并改变栈顶指针 $top$ 的指向位置。
获取栈顶元素:相当于获取线性表中最后一个数据元素。与插入元素、删除元素不同的是,该操作并不改变栈顶指针 $top$ 的指向位置。
接下来我们来看一下栈的顺序存储与链式存储两种不同的实现方式。
堆栈最简单的实现方式就是借助于一个数组来描述堆栈的顺序存储结构。在 Python 中我们可以借助列表 $list$ 来实现。这种采用顺序存储结构的堆栈也被称为 「顺序栈」。
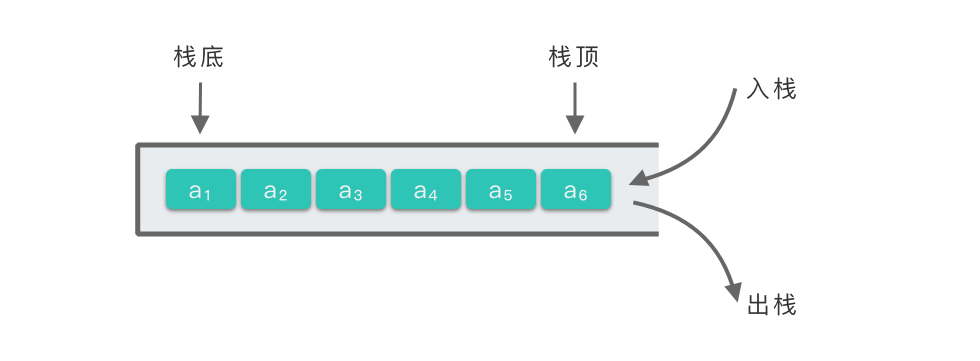
我们约定 $self.top$ 指向栈顶元素所在位置。
class Stack:
# 初始化空栈
def __init__(self, size=100):
self.stack = []
self.size = size
self.top = -1
# 判断栈是否为空
def is_empty(self):
return self.top == -1
# 判断栈是否已满
def is_full(self):
return self.top + 1 == self.size
# 入栈操作
def push(self, value):
if self.is_full():
raise Exception('Stack is full')
else:
self.stack.append(value)
self.top += 1
# 出栈操作
def pop(self):
if self.is_empty():
raise Exception('Stack is empty')
else:
self.stack.pop()
self.top -= 1
# 获取栈顶元素
def peek(self):
if self.is_empty():
raise Exception('Stack is empty')
else:
return self.stack[self.top]
堆栈的顺序存储结构保留着顺序存储分配空间的固有缺陷,即在栈满或者其他需要重新调整存储空间时需要移动大量元素。为此,堆栈可以采用链式存储方式来实现。在 Python 中我们通过构造链表节点 $Node$ 的方式来实现。这种采用链式存储结构的堆栈也被称为 「链式栈」。
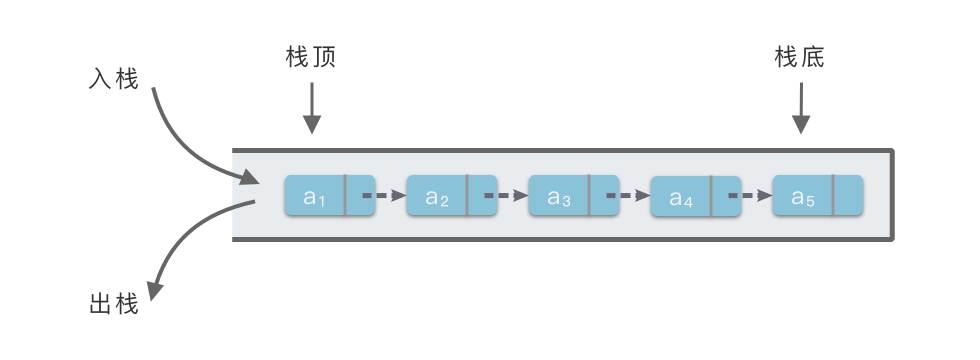
我们约定 $self.top$ 指向栈顶元素所在位置。
class Node:
def __init__(self, value):
self.value = value
self.next = None
class Stack:
# 初始化空栈
def __init__(self):
self.top = None
# 判断栈是否为空
def is_empty(self):
return self.top == None
# 入栈操作
def push(self, value):
cur = Node(value)
cur.next = self.top
self.top = cur
# 出栈操作
def pop(self):
if self.is_empty():
raise Exception('Stack is empty')
else:
cur = self.top
self.top = self.top.next
del cur
# 获取栈顶元素
def peek(self):
if self.is_empty():
raise Exception('Stack is empty')
else:
return self.top.value
堆栈是算法和程序中最常用的辅助结构,其的应用十分广泛。堆栈基本应用于两个方面:
下面我们来讲解一下栈应用的典型例子。
描述:给定一个只包括 '(',')','{','}','[',']' 的字符串 $s$。
要求:判断字符串 $s$ 是否有效(即括号是否匹配)。
说明:
示例:
输入:s = "()"
输出:True
输入:s = "()[]{}"
输出:True
括号匹配是「栈」的经典应用。我们可以用栈来解决这道题。具体做法如下:
class Solution:
def isValid(self, s: str) -> bool:
if len(s) % 2 == 1:
return False
stack = list()
for ch in s:
if ch == '(' or ch == '[' or ch == '{':
stack.append(ch)
elif ch == ')':
if len(stack) !=0 and stack[-1] == '(':
stack.pop()
else:
return False
elif ch == ']':
if len(stack) !=0 and stack[-1] == '[':
stack.pop()
else:
return False
elif ch == '}':
if len(stack) !=0 and stack[-1] == '{':
stack.pop()
else:
return False
if len(stack) == 0:
return True
else:
return False
描述:给定一个字符串表达式 $s$,表达式中所有整数为非负整数,运算符只有 +、-、*、/,没有括号。
要求:实现一个基本计算器来计算并返回它的值。
说明:
+、-、*、/)组成,中间由一些空格隔开。示例:
输入:s = "3+2*2"
输出:7
输入:s = " 3/2 "
输出:1
计算表达式中,乘除运算优先于加减运算。我们可以先进行乘除运算,再将进行乘除运算后的整数值放入原表达式中相应位置,再依次计算加减。
可以考虑使用一个栈来保存进行乘除运算后的整数值。正整数直接压入栈中,负整数,则将对应整数取负号,再压入栈中。这样最终计算结果就是栈中所有元素的和。
具体做法:
+。+,则将 $num$ 压入栈中。-,则将 $-num$ 压入栈中。*,则将栈顶元素 $top$ 取出,计算 $top \times num$,并将计算结果压入栈中。/,则将栈顶元素 $top$ 取出,计算 $int(top / num)$,并将计算结果压入栈中。+、-、*、/ 操作符,则更新 $op$。class Solution:
def calculate(self, s: str) -> int:
size = len(s)
stack = []
op = '+'
index = 0
while index < size:
if s[index] == ' ':
index += 1
continue
if s[index].isdigit():
num = ord(s[index]) - ord('0')
while index + 1 < size and s[index+1].isdigit():
index += 1
num = 10 * num + ord(s[index]) - ord('0')
if op == '+':
stack.append(num)
elif op == '-':
stack.append(-num)
elif op == '*':
top = stack.pop()
stack.append(top * num)
elif op == '/':
top = stack.pop()
stack.append(int(top / num))
elif s[index] in "+-*/":
op = s[index]
index += 1
return sum(stack)
此处可能存在不合适展示的内容,页面不予展示。您可通过相关编辑功能自查并修改。
如您确认内容无涉及 不当用语 / 纯广告导流 / 暴力 / 低俗色情 / 侵权 / 盗版 / 虚假 / 无价值内容或违法国家有关法律法规的内容,可点击提交进行申诉,我们将尽快为您处理。