当然，以下是一个这篇文章的简单的文字版的思维导图：

1.勾股定理
五百多种证法
与圆的关系
直角三角形
证明
应用

2.圆
定理
应用范围
与勾股定理的关系

3.直角三角形
重要定理：勾股定理
与圆的关系
辅助线
三边关系

4.证明
辅助圆
勾股定理多种证法
5.联想

分析能力
自主学习
从问题出发

6.认识
对勾股定理和圆的新认识
数学世界之宏大

好的，以下是基于所提供的思维导图的多级目录：

1. 概述

   • 勾股定理简介和历史
   • 圆的概念和特征
   • 直角三角形的性质和分类

2. 勾股定理

   • 证明
     • 直观证明
     • 代数证明
     • 几何证明
     • 其他证明
   • 应用
     • 求直角三角形的边长和角度
     • 解决实际问题
     • 求解勾股三元组
   • 扩展应用
     • 平面几何中的应用
     • 空间几何中的应用

3. 圆

   • 圆的定义和性质
   • 圆内接四边形定理
   • 圆的切线定理
   • 圆的割线定理
   • 圆的三角形定理

4. 直角三角形

   • 证明勾股定理
     • 辅助圆法
     • 周公法
     • 均分线法
   • 直角三角形的性质
     • 正弦定理
     • 余弦定理

教师说：
张炜杰同学从日常的学习中展开丰富的联想，与自主学习内容建立联系，从问题出发，不断地思考解决问题的过程展示他强大的分析能力。

思考与收获：
收获：本次证明中我使用了辅助圆的方式，对勾股定理进行了多种方式的证明。在这个过程中我的收获有：

1. 对圆的各个定理有了新的认识，发现圆的应用范围不止在和圆有关的命题中；
2. 对勾股定理有了一个新的认识，了解到了这个古老定理涉及的知识面之广，范围之大；
3. 对数学的世界有了新的认识，仅仅勾股定理的有关圆的证法就有这么多种，而这只是冰山的一片雪花，让我明白了数学的宏大。

证法一（邹元治证明）：
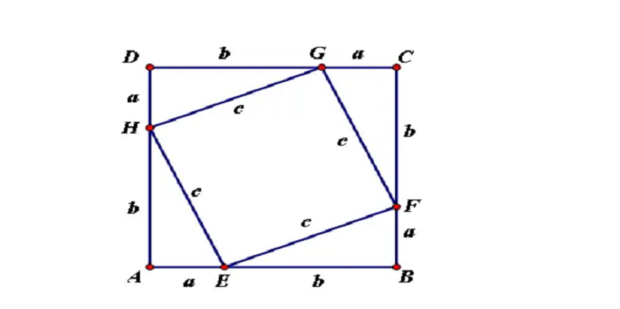
以a、b为直角边，以c为斜边做四个全等的三角形，按下图所示相拼，使A、E、B三点共线，B、F、C 三点共线，C、G、D三点共线。
∵Rt△HAE≌Rt△EBF
∴∠AHE=∠BEF
∵∠AHE+∠AEH=90°
∴∠BEF+∠AEH=90°
∵A、E、B共线
∴∠HEF=90°，四边形EFGH为正方形
由于上图中的四个直角三角形全等，易得四边形ABCD为正方形
∴正方形ABCD的面积=四个直角三角形的面积+正方形EFGH的面积
∴(a+b)^2=4•（1/2）•ab+c^2，整理得a^2+b^2=c^2

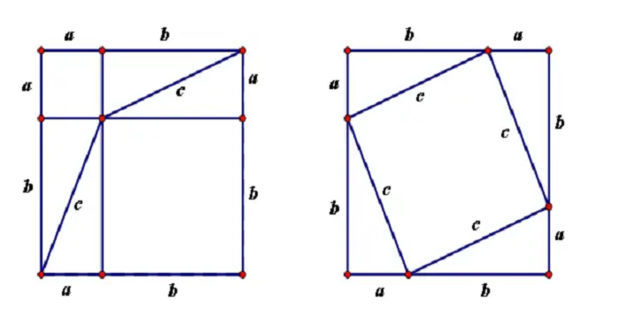
证法二（课本的证明）：
如上图所示两个边长为a+b的正方形面积相等，
所以a^2+b^2+4•（1/2）•ab=c^2+4•（1/2）•ab，故a^2+b^2=c^2。

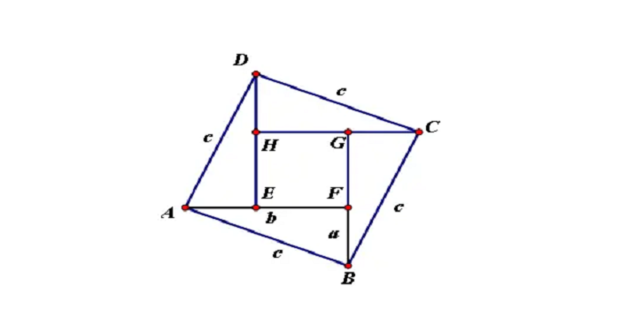
证法三（赵爽弦图证明）：
以a、b为直角边，以c为斜边做四个全等的三角形，按下图所示相拼。
易得四边形ABCD和四边形EFGH都是正方形
∴正方形ABCD的面积=四个直角三角形的面积+正方形EFGH的面积
∴c^2=4•（1/2）•ab+(b-a)^2 ，整理得a^2+b^2=c^2

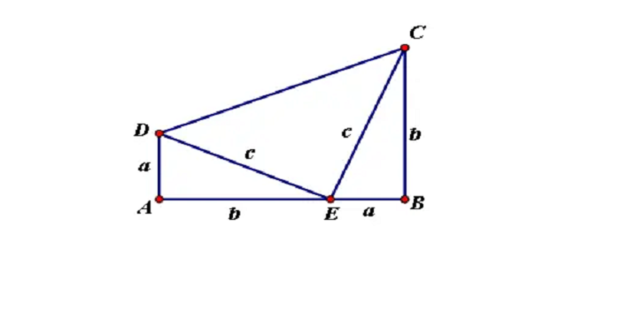
证法四（总统证明）：
如下图所示。
易得△CDE为等腰直角三角形
∴梯形ABCD的面积=两个直角三角形的面积+一个等腰三角形的面积
∴1/2•（a+b）•（a+b）=2•（1/2）•ab+（1/2）•c^2，整理得a^2+b^2=c^2

证法五（梅文鼎证明）：
以a、b为直角边，以c为斜边做四个全等的三角形，按下图所示相拼，使DEF在同一直线上，过C点作CI垂直于DF,交DF于I点。
易得四边形ABEG、四边形CBDI、四边形FGHI都为正方形。
∴多边形EGHCB的面积=正方形ABEG的面积-两个直角三角形的面积
且多边形EGHCB的面积=正方形CBDI的面积+正方形FGHI的面积-两个直角三角形的面积
∴正方形ABEG的面积=正方形CBDI的面积+正方形FGHI的面积
∴c²=a²+b²

证法六（项明达证明）：
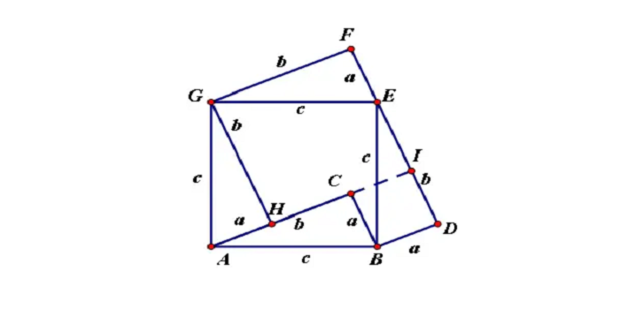
以a、b为直角边，以c为斜边做两个全等的三角形，做一个边长为c的正方形，按下图所示相拼，使E、A、C在同一条直线上。
过Q点作QP⊥AC，交AC于P点
分别过F、B作QP的垂线段，交点分别为M、N
易得四边形ABQF为正方形
利用全等三角形的判定定理角角边（AAS）可得
△AEF≌△QMF≌△BNQ，此时问题转化为梅文鼎证明。

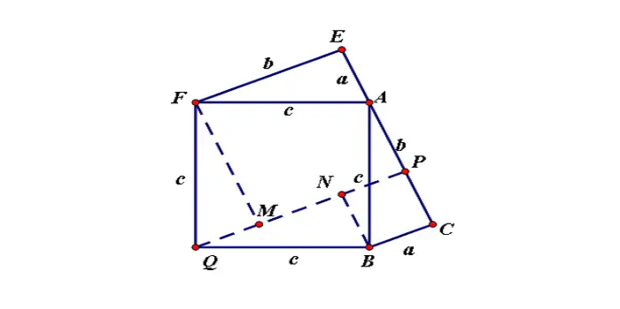
证法七（欧几里得证明）：
在直角边为a、b，斜边为c的直角三角形中，分别以a、b、c为边作正方形，如下图所示。连接FB和CD，过C点作CN⊥DE交DE于E点，交AB于M点。
∵AF=AC，AB=AD，∠FAB=∠CAD，∴△FAB≌△CAD（SAS）
而△FAB的面积=△CAD的面积=（½）•ac sin（90°+∠CAB）=（½）a²
∵△CAD与矩形AMND等底等高
∴矩形AMND的面积为△CAD面积的两倍，即a²
同理可得矩形BMNE的面积为b²
∵正方形ADEB的面积=矩形AMND的面积+矩形BMNE的面积
∴c²=a²+b²

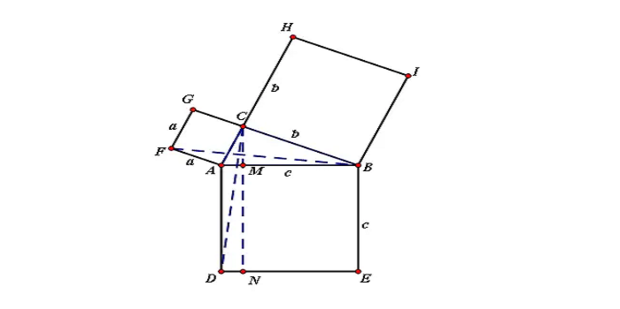
证法八（相似三角形性质证明）
如下图所示，在直角三角形ABC中，AC=b，BC=a，AB=c,∠ACB=90°，过C点作CD垂直于AB，交AB于D点。
∵∠BDC=∠BCA=90°，∠B=∠B
∴△BDC∽△BCA
∴BD∶BC=BC∶BA
∴BC²=BD•BA
同理可得AC²=AD•AB
∴BC²+AC²=BD•BA+AD•AB=(BD+AD)•AB=AB²,即a²+b²=c²

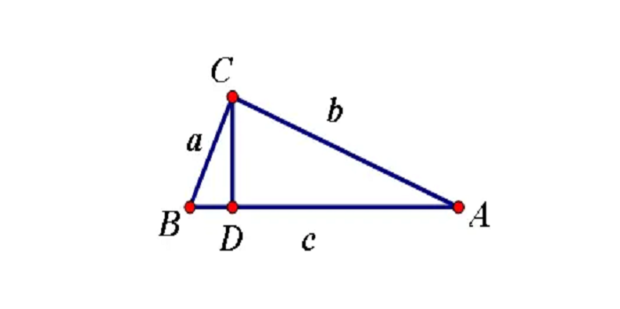
证法九（杨作玫证明）：
做两个全等的直角三角形，设它们的两直角边分别为a、b（b>a）斜边长为c，再做一个边长为c的正方形，按下图所示相拼。过A点作AG⊥AC，交DF于G点，AG交DE于H点。过B作BI⊥AG，垂足为I点。过E点作EJ与CB的延长线垂直，垂足为J点，EJ交AG于K点,交DB于L点。
∵∠BAE=90°∠GAC=90°∴∠EAK=∠BAC
∵GA⊥AC,BC⊥AC
∴GA∥BC
∵EJ⊥BC
∴EJ⊥GA
∴∠EKA=∠C=90°而AE=AB=c
∴△EAK≌△BAC（AAS）
∴EK=a，KA=b
由作法易得四边形BCAI为矩形
∴AI=a,KI=b-a
∵△BAC≌△EDF
∴△EAK≌△EDF
∴∠FED=∠KEA
∴∠FEK=90°
∴四边形EFGK为正方形，同时四边形DGIB为直角梯形
用数字表示面积的编号（如图），则以c为边长的正方形的面积为
c²=S1+S2+S3+S4+S5 ①
∵S8+S3+S4=½[b+(b-a)]•[a+(b-a)]
=b²-½ab ，S5=S8+S9
∴S3+S4=b²-½ab-S8=b²-S1-S8②
把②代入①得
c²=S1+S2+b²-S1-S8+S8+S9
=b²+S2+S9
=b²+a²

证法十（李锐证明）：
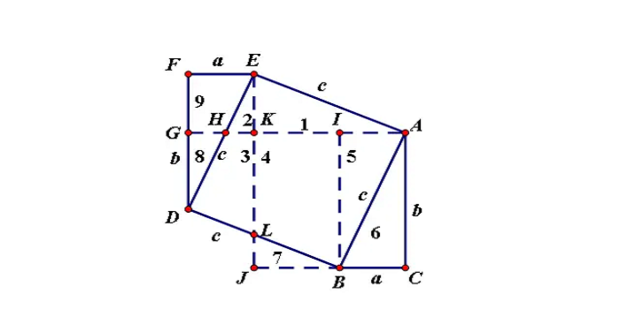
设直角三角形两直角边长分别为a、b（b>a）,斜边长为c。做三个边长分别为a、b、c的正方形，按下图相拼，使AEG三点共线，过Q点作GM⊥AG,交点为M,用数字表示面积的编号。
∵∠TBE=∠ABH=90°
∴∠TBH=∠EBA
∵∠T=∠BEA=90°，BT=BE=b
∴△HBT≌△ABE（ASA）
∴HT=AE=a，GH=GT-HT=b-a
∵∠GHF+∠BHT=90°，∠TBH+∠BHT=90°
∴∠GHF=∠TBH=∠DBC
∵BD=BE-ED=b-a，
∠G=∠BDC=90°
∴△GHF≌△DBC（ASA），S7=S2
由∠BAQ=∠BEA=90°,可知∠ABE=∠QAM
∵AB=AQ=c
∴△ABE≌△QAM（AAS）
∴△QAM≌△HBT，S5=S8
同时有AR=AE=QM=a，且∠QFM与∠ACR分别为∠GHF与∠DBC的余角
∴∠QFM=∠ACR
∵∠R=∠FMQ=90°
∴△FMQ≌△CRA（AAS），S4=S6
∵c²=S1+S2+S3+S4+S5,
a²=S1+S6,b²=S3+S7+S8
S7=S2,S8=S5,S4=S6
∴a²+b²=S1+S6+S3+S7+S8=S1+S4+S3+S2+S5=c²

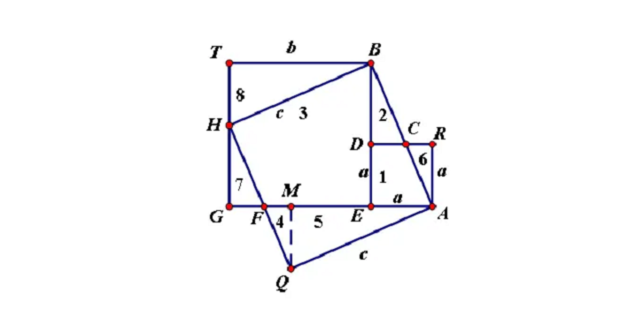
证法十一（利用切割线定理证明）：
在直角三角形ABC中，∠ACB=90°，AC=b，AB=c，BC=a，以B为圆心，a为半径画圆，AB交圆与D点，AB的延长线交圆于E点。
根据切割线定理（从圆外一点引圆的切线和割线，切线长是割线和这点到割线与圆交点的两条线段长的比例中项）可得：AC²=AD•AE
∴b²=(c-a)(c+a)=c²-a²
∴a²+b²=c²
[Image is uploading…(image-WgQSi8BEXrFdDD0CvkLt)]

证法十二（利用多列米定理证明）：
在直角三角形ABC中，设BC=a，AC=b，斜边AB=c，过A点作AD∥CB,过B点作BD∥CA,则四边形ACBD为矩形，矩形ACBD内接于唯一的一个圆。
根据多米列定理（圆内接四边形对角线的乘积等于两对边乘积之和）可得：
AB•DC=DB•AC+AD•CB
∵AB=DC=c,DB=AC=b，AD=CB=a
∴c²=b²+a²

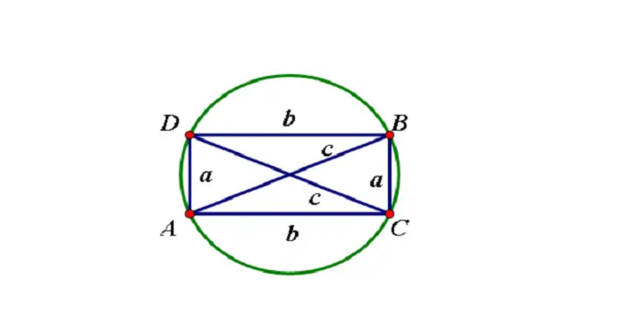
证法十三（作直角三角形的内切圆证明）：
在Rt△ABC中，设直角边BC=a，AC=b，斜边AB=c。作Rt△ABC的内切圆⊙O，切点分别为D、E、F，如下图所示，设圆O的半径为r。
∵AB=AF＋BF,CB=BD＋CD,AC=AE＋CE
∴AC+CB-AB=(AE+CE)+(BD+CD)-(AF+BF)=CE+CD=2r,即a+b-c=2r
∴a+b=2r+c
(a+b)²=(2r+c)²
a²+b²+2ab=4(r²+rc)+c²
∵S△ABC=½ab
∴4S△ABC=2ab
∵S△ABC=S△AOB+S△BOC+S△AOC=½cr+½ar+½br=½(a+b+c)r=½(2r+c+c)r=r²+rc
∴4(r²+rc)=2ab
∴a²+b²+2ab=2ab+c²
∴a²+b²=c²

证法十四（利用反证法证明）：
在Rt△ABC中，设直角边BC=a，AC=b，斜边AB=c。过C点作CD⊥AB，垂足为D点，如下图所示。
假设a²+b²≠c²，即AC²+BC²≠AB²
则由AB²=AB·AB=AB·(AD+BD)=AB·AD+AB·BD知
AC²≠AB·AD或BC²≠AB·BD
即AD∶AC≠AC∶AB或BD∶BC≠BC∶AB
在△ADC和△ACB中
∵∠A=∠A
∴若AD∶AC≠AC∶AB，则∠ADC≠∠ACB
在△CBD和△ACB中
∵∠B=∠B
∴若BD∶BC≠BC∶AB，则∠CDB≠∠ACB
∵∠ACB=90°
∴∠ADC≠90°，∠CDB≠90°
这与CD⊥AB矛盾，所以假设不成立
∴a²+b²=c²

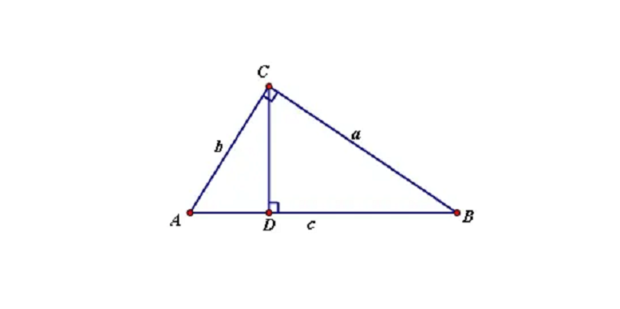
证法十五（辛卜松证明）：
直角三角形以a、b为直角边，以c为斜边。作边长为a+b的正方形。
把正方形ABCD划分成上方左图所示的几个部分，则正方形ABCD的面积为
(a+b)²=a²+b²+2ab
把正方形ABCD划分成上方右图所示的几个部分，则正方形ABCD的面积为
(a+b)²=4x½ab+c²=2ab+c²
∴a²+b²+2ab=2ab+c²
∴a²+b²=c²
[Image is uploading…(image-a8TEW6uFDITTqZ4kuv3g)]

证法十六（陈杰证明）：
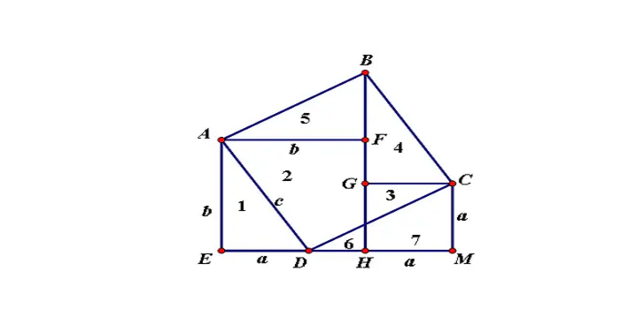
设直角三角形两直角边的长分别为a、b（b>a），斜边的长为c。做两个边长分别为a、b的正方形，把它们拼成如图所示形状，使E、H、M三点在一条直线上。 用数字表示面积的编号，如下图所示。
在EH = b上截取ED = a，连结DA、DC，则 AD = c
∵ EM = EH + HM = b + a , ED = a
∴ DM = EM―ED = (b+a)―a = b
又∵ ∠CMD = 90°，CM = a， ∠AED = 90°， AE = b
∴ RtΔAED ≌ RtΔDMC(SAS)
∴ ∠EAD = ∠MDC，DC = AD = c
∵ ∠ADE + ∠ADC+ ∠MDC =180°， ∠ADE + ∠MDC = ∠ADE + ∠EAD = 90°
∴ ∠ADC = 90°
∴ 作AB∥DC，CB∥DA，则四边形ABCD是一个边长为c的正方形
∵ ∠BAF + ∠FAD = ∠DAE + ∠FAD = 90°
∴ ∠BAF=∠DAE。连结FB，在ΔABF和ΔADE中
∵ AB =AD = c，AE = AF = b，∠BAF=∠DAE
∴ ΔABF ≌ ΔADE(SAS)
∴ ∠AFB = ∠AED = 90°，BF = DE = a
∴ 点B、F、G、H在一条直线上
在RtΔABF和RtΔBCG中，
∵ AB = BC = c，BF = CG = a，
∴ RtΔABF ≌ RtΔBCG (HL)
∵c²=S₂+S₃+S₄+S₅， b²=S₁+S₂+S₆， a²=S₃+S₇，S₁=S₅=S₄=S₆+S₇，
∴a²+b²=S₃+S₇+S₁+S₂+S₆=S₂+S₃+S₁+(S₆+S₇)=S₂+S₃+S₄+S₅ =c²
∴ a²+b²=c²

Babylonian tablets suggest Pythagorean Theorem used 1,000 years before ...
wildhunt.org|1062 × 1164 jpeg|Image may be subject to copyright.