# Deep Learning
**Repository Path**: fakerlove/deep-learning
## Basic Information
- **Project Name**: Deep Learning
- **Description**: 深度学习知识库,
深度学习的所有内容
- **Primary Language**: Unknown
- **License**: Not specified
- **Default Branch**: master
- **Homepage**: None
- **GVP Project**: No
## Statistics
- **Stars**: 2
- **Forks**: 6
- **Created**: 2021-07-15
- **Last Updated**: 2024-11-25
## Categories & Tags
**Categories**: Uncategorized
**Tags**: None
## README
# 深度学习
[文章代码原文链接](https://gitee.com/fakerlove/deep-learning)
~~~bash
https://gitee.com/fakerlove/deep-learning
~~~
学习路线
[1-----python](https://gitee.com/fakerlove/python)
[2----常见的深度学习框架](https://gitee.com/fakerlove/deep-learning)
[3-----pytorch学习](https://gitee.com/fakerlove/pytorch)
[4----CV领域学习](https://gitee.com/fakerlove/cv)




 # 0. 概述
## 0.1 概念
很多人都有误解,以为深度学习比机器学习先进。其实深度学习是机器学习的一个分支。
可以理解为具有多层结构的模型。具体的话,深度学习是机器学习中的具有深层结构的神经网络算法,即机器学习>神经网络算法>深度神经网络(深度学习)。
深度学习(deep learning,以下简称DL),换种说法,可以说是基于人工神经网络的机器学习。区别于传统的机器学习,DL需要更多样本,换来更少的人工标注和更高的准确率。
传统的BP神经网络一般指三层的全连接神经网络,而大于三层就成了DNN(深度神经网络)。
事实上,DNN能解决一些问题,但因为参数太多,逐步被其他网络模型取代:CNN(卷积神经网络)、RNN(循环神经网络)。二者目前最成功的实现分别是ResNet和LSTM。
深度学习三巨头
* 神经网络之父**hinton**
* 卷积神经网络之父**lecun**
* GAN网络之父**bengio**
LSTM 之父 Jürgen Schmidhuber
## 0.2 历史
* 第一代`神经网络`又称为`感知器`,由科学家Frank Rosenblatt发明于1950至1960年代,它的算法只有两层,输入层输出层,,主要使用的是一种叫做sigmoid神经元(sigmoid neuron)的神经元模型,主要是线性结构。它不能解决线性不可分的问题,如异或操作。
* 为了解决第一代神经网络的缺陷,在`1980年左右`提出第二代神经网络`多层感知器(MLP)`。和第一代神经网络相比,第二代在输入输出层之间有增加了隐含层的感知机,引入一些非线性的结构,解决了之前无法模拟异或逻辑的缺陷。第二代神经网络让科学家们发现神经网络的层数直接决定了它对现实的表达能力,但是随着层数的增加,优化函数愈发容易出现局部最优解的现象,由于存在梯度消失的问题,深层网络往往难以训练,效果还不如浅层网络。
* 2006年`Hinton`采取无监督预训练(Pre-Training)的方法解决了梯度消失的问题,使得深度神经网络变得可训练,将隐含层发展到7层,有一个预训练的过程。使用微调技术作为反向传播和调优手段。减少了网络训练时间,并且提出了一个新的概念叫做"`深度学习`",直到2012年,在`ImageNet竞赛`中,`Hinton教授的团队`,使用以卷积神经网络为基础的深度学习方案,他们训练的模型面对15万张测试图像时,预测的头五个类别的错误率只有 15.3%,而排名第二的日本团队,使用的SVM方法构建的模型,相应的错误率则高达 26.2%。从此一战成名!2012年后深度学习就成为主流。
# 1. 感知机
资料参考
~~~bash
https://blog.csdn.net/m0_37957160/article/details/113922919
~~~
资料参考2
~~~bash
https://blog.csdn.net/Insincerity/article/details/106446689
~~~
资料参考3
~~~bash
https://www.jianshu.com/p/81fa7682daf3
~~~
## 1.1 概念
感知机是1957年,由Rosenblatt提出会,是**神经网络和支持向量机**的基础。
感知机是**二分类**的线性分类模型,输入为实例的特征向量,输出为实例的类别(取+1和-1)。感知机对应于输入空间中将**实例划分为两**类的分离超平面。感知机旨在求出该超平面,为求得超平面导入了基于误分类的损失函数,利用梯**度下降法对损失函数进行最优化**。
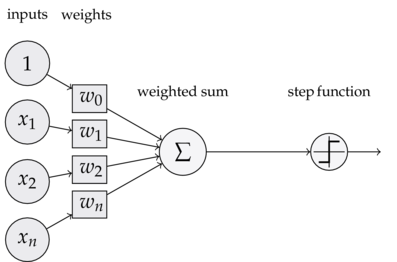
## 1.2 算法模型
### 1.2.1 模型
输入:$x\in R^n$,x是特征向量
输出:$Y\in \{-1,1\}$
由输入空间到输出空间的表达形式为:
$y=sign(w\times x+b)$
**上面该函数称为感知机,其中w,b称为模型的参数,$w\in R^n$称为权值,b称为偏置,$w\times x$表示为w,x的内积**
$$
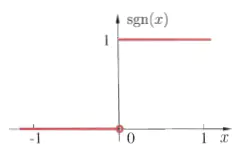
f(n)=\begin{cases}1,if\quad n\ge 0\\ 0,otherwise\end{cases}
$$
下面是符号函数的函数图像(w为一维的数据量$w=[w_1]$):
### 1.2.2 分离超平面
感知机的作用就是找到一个分离超平面,使数据能够正确分为两类。
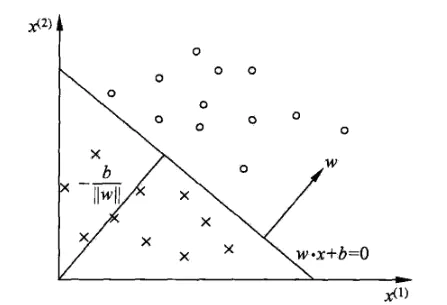
在实际情况中,w往往是$w=\begin{bmatrix}w_1\\ w_2\\ \vdots\\ w_n\end{bmatrix}$,多维的。这个时候$w\times x+b$表示的是超平面
在感知机中,一般把超平面方程写为:wx+b=0.
w 为超平面的法向量,b 是超平面的截距,超平面把数据分为两类,如下图。
### 1.2.3 损失函数
感知机能够自动地把 w 和 b 求解出来,求解过程中有个重点,就是**损失函数**的引入,损失函数也叫代价函数,是样本分类预测结果和样本实际类别差异的度量,正是通过最小化损失函数,感知机才能不断地修正w和b的值,找到一个最优的超平面。
1. 超平面的距离
感知机中的损失函数是所有误分类点到分离超平面的距离,其中,某一个误分类点到超平面的距离表示为:
$\frac{1}{||w||}|w\cdot x_0+b|$
$||w||$是$w$的$L_2$范数,这个**L2范数**乍听有点高大上,实际上就是 w 中每个元素去平方,然后相加开根号
$||w||=\sqrt{w_1^2+w_2^2+\dots+w_n^2}$
2. 误分类点到分离超平面的距离
对于一个误分类数据$(x_i,y_i)$,当 $w \cdot x_i + b > 0$ 时,$y_i =-1$;当$w\cdot x_i + b < 0$时,$y_i =1$;所以$y_i*(w\cdot x_i + b)>0$,所有误分类点到分离超平面的距离为:
$-\frac{1}{||w||}\sum_{x_i\in M}y_i(w\cdot x_i+b),M是误分类集合$
为啥距离是这个呢???,
$因为y_i=1或-1,不改变结果,只改变正负$
不考虑$\frac{1}{||w||}$损失函数写成这样:
$L(w,b)=-\sum_{x_i\in M}y_i(w\cdot x_i+b)$
我们的目标就是最小化损失函数 L(w,b),这里用 **随机梯度下降(SGD)**的方法来做最小化。
> L0范数是指向量中非0的元素的个数。(L0范数很难优化求解)
>
> L1范数是指向量中各个元素绝对值之和
>
> L2范数是指向量各元素的平方和然后求平方根
### 1.2.4 随机梯度下降
梯度下降方向就是梯度的反方向,最小化损失函数 L(w,b) 就是先求函数在 w 和 b 两个变量轴上的偏导:
$\nabla_wL(w,b)=-\sum_{x_i\in M}y_ix_i$
$\nabla_bL(w,b)=-\sum_{x_i\in M}y_i$
上面的式子,每更新一次参数,需要遍历整个数据集,如果数据集非常大的话,显然是不合适的,为了解决这个问题,只随机选取一个误分类点进行参数更新,这就是**随机梯度下降(SGD)**,如下所示。
$w+\eta y_ix_i\to w$
$b+\eta y_i\to b$
这里的 η 指的是**学习率**,相当于控制下山的步幅,$\eta$ 太小,函数拟合(收敛)过程会很慢,$\eta$太大,容易在最低点方向震荡,进入死循环。
当没有误分类点的时候,停止参数更新,所得的参数就是感知机学习的结果,这就是**感知机的原始形式**。下面总结一下参数更新的过程:
(1)预先设定一个$w_0$和$b_0$,即w和b的初值。
(2)在训练集中选取数据$(x_i,y_i)$。
(3)当$y_i*(w\cdot x_i +b)\le 0$时,利用随机梯度下降算法进行参数更新。
#### 例子
> 输入:正例$x_1=[3,3]^T,x_2=[4,3]^T,负例x_3=[1,1]^T。$
>
> 输出:感知机模型$f(x)=sign(w\times x+b)$
目标公式$min_{w,b}=-\sum_{x_i\in M}y_i(w\cdot x+b)$
* 假设$w_0=\begin{bmatrix}0&0\end{bmatrix},\eta=1,b_0=0$
* 判断$x_1$是否正确分类,$y_1(w_0\cdot x_1+b)=\begin{bmatrix}0&0\end{bmatrix}\begin{bmatrix}3\\ 3\end{bmatrix}+0=0$不能正确分类
更新$w,b$
* 更新公式为$w+\eta y_ix_i\to w$
$w_1=w_0+\eta y_1x_1=\begin{bmatrix}0&0\end{bmatrix}+1\times 1\times \begin{bmatrix}0&0\end{bmatrix}=\begin{bmatrix}3&3\end{bmatrix}$
同理$b_1=b_0+y_1=1$,得到新的模型$w_1\cdot x+b_1$
* 更新后的模型,对于$x_1,x_2$被正确分类,但是对于$x_3$错误分类。进行更新$w_1,b_1$
$w_2=w_1+\eta y_3x_3=\begin{bmatrix}0&0\end{bmatrix}+1\times (-1)\times \begin{bmatrix}1&1\end{bmatrix}=\begin{bmatrix}2&2\end{bmatrix}$$b_2=0$
依次类推
迭代过程如下
| 迭代次数 | 误分类点 | w | b | wx+b |
| -------- | -------- | --------------------------------- | ---- | ---- |
| 0 | | $\begin{bmatrix}0&0\end{bmatrix}$ | 0 | |
| 1 | $x_1$ | $\begin{bmatrix}3&3\end{bmatrix}$ | -1 | |
| 2 | $x_3$ | $\begin{bmatrix}2&2\end{bmatrix}$ | 0 | |
| 3 | $x_3$ | $\begin{bmatrix}1&1\end{bmatrix}$ | -1 | |
| 4 | $x_3$ | $\begin{bmatrix}0&0\end{bmatrix}$ | -2 | |
| 5 | $x_1$ | $\begin{bmatrix}3&3\end{bmatrix}$ | -1 | |
| 6 | $x_3$ | $\begin{bmatrix}2&2\end{bmatrix}$ | -2 | |
| 7 | $x_3$ | $\begin{bmatrix}1&1\end{bmatrix}$ | -3 | |
| 8 | 0 | $\begin{bmatrix}1&1\end{bmatrix}$ | -3 | |
### 1.2.5 对偶形式
将 w 和 b 表示为实例$x_1$和标记$y_1$线性组合的形式,通过求解系数来求解w和b,前面提到过这个式子:
$w+\eta y_ix_i\to w$
$b+\eta y_i\to b$
这里先假设 w 和 b 的初值为0,那么通过对偶形式能表示为什么?从上面式子可以看出来,每次迭代,w会增加一个 $ηy_ix_i$,b 会增加一个$ηy_i$,到最后参数更新完之后,w 和 b 一共增加了这些:
$w=\sum_{i=1}^N\alpha_iy_ix_i$
$b=\sum_{i=1}^N\alpha_iy_i$
这里的$α_i = n_i*η$,$n_i$就是$(x_i,y_i)$被误分类的次数,η 还是学习率。
$\alpha_i$越大,意味这实例点更新次数越多,距离分离超平面越近,越难被分类,对实例影响结果越大
下面是对偶形式的参数更新过程:
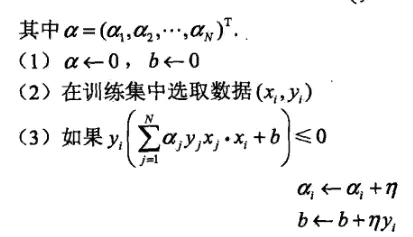
## 1.3 逻辑电路
### 1.3.1 与门
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
### 1.3.2 与非门
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
### 1.3.3 或门
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
### 1.3.4 异或门
什么是异或?就是,假如这里有两件事,一真一假,异或为真;两件事都为假或者两件事都为真,异或为假,就像这样:
0⊕0=0,0⊕1=1
1⊕0=1,1⊕1=0
下面是异或的函数图像:
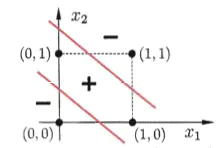
通过图像可以看出,找不到一个超平面能将这四个点分隔开,所以**感知机无法处理异或问题,不仅仅是感知机,其他线性模型也无法处理这种问题。**
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
#### 多层感知机mlp
如何解决呢???
使用多层的感知机即可完成,如下图所示
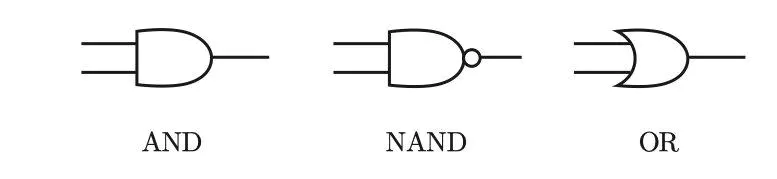
与门、与非门、或门的符号
通过上面的感知机如何组成异或门呢??
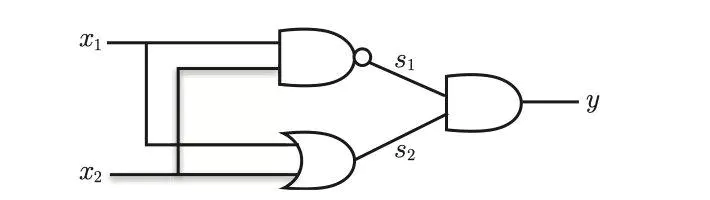
这里,把$s_1$作为 与非门 的输出,把$s_2$ 作为或门的输出,填入真值表中。
结果如图所示,观察$x_1、x_2 、y$,可以发现确实符合异或门的输出
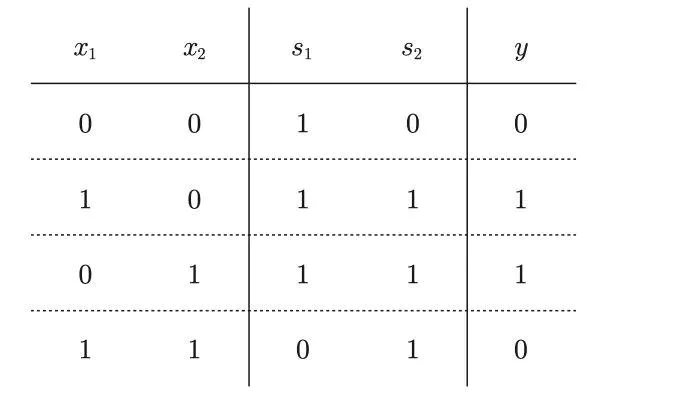
异或门是一种多层结构的神经网络。
与门、或门是单层感知机,而异或门是2层感知机。叠加了多 层的感知机也称为多层感知机(multi-layered perceptron) 。
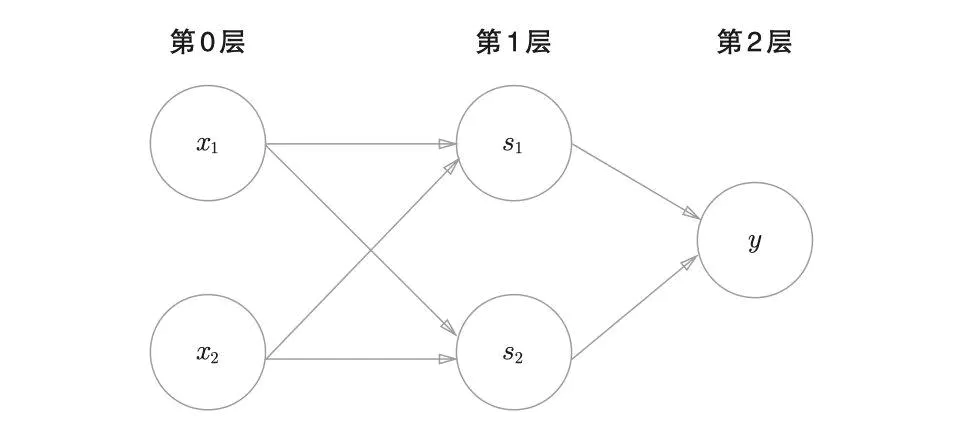
**感知机的作用就是引出神经网络**
# 2. 神经网络
参考资料
~~~bash
https://blog.csdn.net/as091313/article/details/79080583
~~~
## 2.1 概念
### 2.1.1 概念
人工神经网络(artificial neural network,ANN),简称神经网络(neural network,NN),是一种模仿生物神经网络的结构和功能的数学模型或计算模型。
神经网络是一种**运算模型**,由大量的节点(或称“神经元”)和之间相互的联接构成。
每个节点代表一种特定的输出函数,称为**激励函数、激活函数**(activation function)。
每两个节点间的联接都代表一个对于通过该连接信号的加权值,称之为权重,这相当于人工神经网络的记忆。
网络的输出则依网络的连接方式,权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近,也可能是对一种逻辑策略的表达。
### 2.1.2 应用-分类
神经网络最重要的用途是分类,为了让大家对分类有个直观的认识,咱们先看几个例子:
* 垃圾邮件识别:现在有一封电子邮件,把出现在里面的所有词汇提取出来,送进一个机器里,机器需要判断这封邮件是否是垃圾邮件。
* 疾病判断:病人到医院去做了一大堆肝功、尿检测验,把测验结果送进一个机器里,机器需要判断这个病人是否得病,得的什么病。
* 猫狗分类:有一大堆猫、狗照片,把每一张照片送进一个机器里,机器需要判断这幅照片里的东西是猫还是狗。
## 2.2 前期准备
资料参考
~~~bash
https://zhuanlan.zhihu.com/p/65472471
~~~
### 2.2.1 神经元
神经网络中最基本的成分是神经元模型,即上述定义中的简单单元
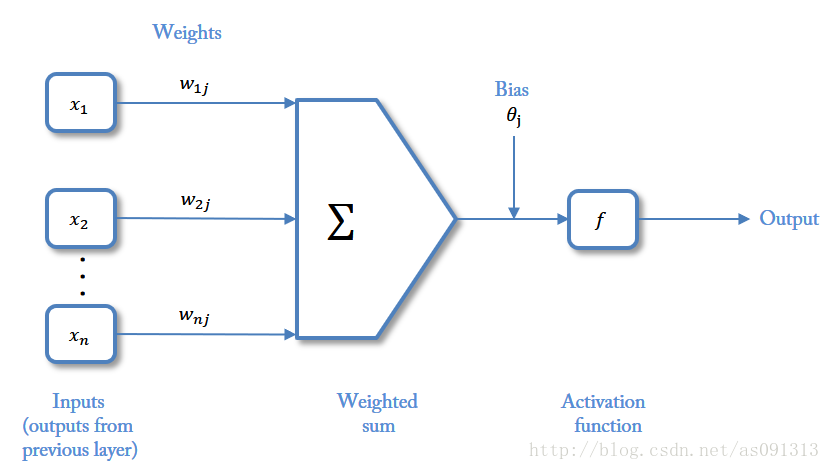
> $Inputs$:输入
>
> $Weights$:权值,权重
>
> $Bias$:偏置,或者称为阈值
>
> $Activationfunction$:激活函数
>
> 这种“阈值加权和”的神经元模型称为**M-P模型** ( McCulloch-Pitts Model ),也称为神经网络的**一个处理单元**( PE, Processing Element )。
### 2.2.2 激活函数
参考资料
~~~bash
https://zhuanlan.zhihu.com/p/25279356
~~~
> 激活函数是用来加入非线性因素的,解决线性模型所不能解决的问题。
>
> 简而言之,激活层是为矩阵运算的结果添加非线性的。
常用的激活函数有三种,分别是阶跃函数、Sigmoid和ReLU。不要被奇怪的函数名吓到,其实它们的形式都很简单,如下图(更正:sigmoid在负无穷是应趋近于0):
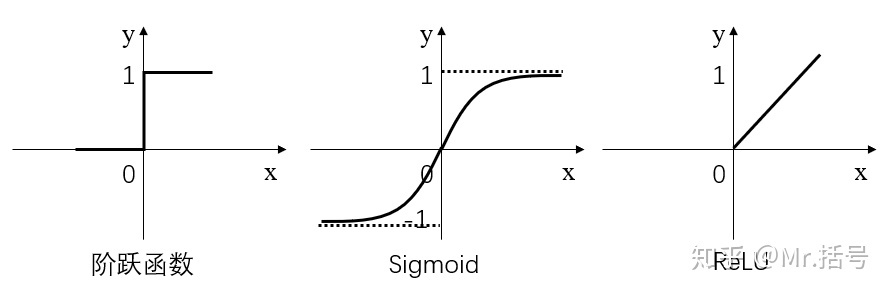
* 阶跃函数:当输入小于等于0时,输出0;当输入大于0时,输出1。
* Sigmoid:当输入趋近于正无穷/负无穷时,输出无限接近于1/0。
* ReLU:当输入小于0时,输出0;当输入大于0时,输出等于输入。
#### 1) sigmoid函数
sigmoid函数是一种常见的挤压函数,其将较大范围的输入挤压到$(0,1)$区间内,其函数的表达式与形状如下图所示:
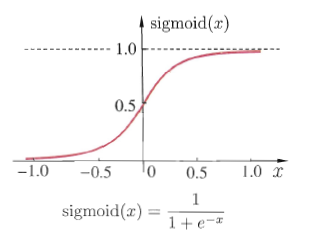
该函数常被用于分类模型,因为其具有很好的一个特性$f^\prime(x)=f(x)(1-f(x))$.这个函数也会被用于下面的神经网络模型中做激活函数。
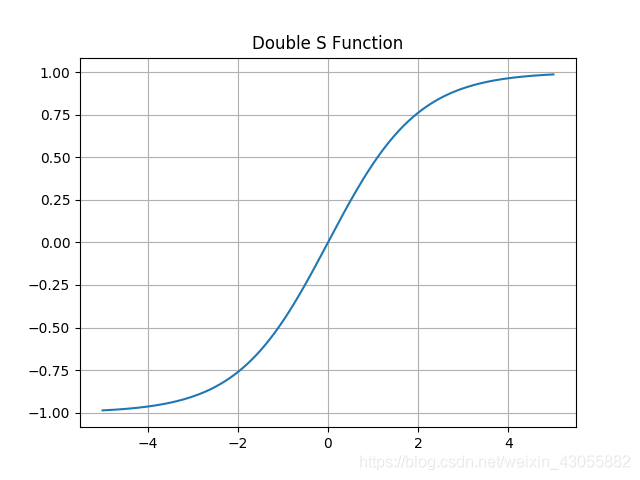
#### 2) 双极性Sigmoid函数
$$
h(x)=\frac{2}{1+e^{-\alpha x}}-1
\\ h^\prime(x)=\frac{2\alpha e^{-\alpha x}}{(1+e^{-\alpha x})}=\alpha\frac{1-h(x)^2}{2}
$$
例子
$f(x)-\frac{1-e^{-x}}{1+e^{-x}}$
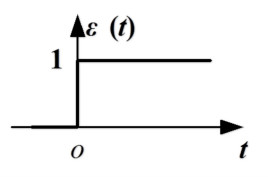
#### 3) 阶跃函数
阶跃函数是一种特殊的连续时间函数,是一个从0跳变到1的过程,属于奇异函数
####
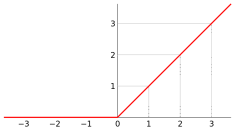
#### 4) ReLU
**线性整流函数**(Rectified Linear Unit, **ReLU**),又称**修正线性单元,**是一种人工神经网络中常用的激活函数(activation function)
### 2.2.3 层介绍
该模型与一个有向无环图相关联
$f(x)=f^{(3)}(f^{(2)}(f^{(1)}(x)))$
$f^{(1)}$被称为网络的第一层,叫做输入层
$f^{(2)}$被称为网络的第二层,叫做隐藏层
$f^{(3)}$被称为网络的第三层,叫做输出层
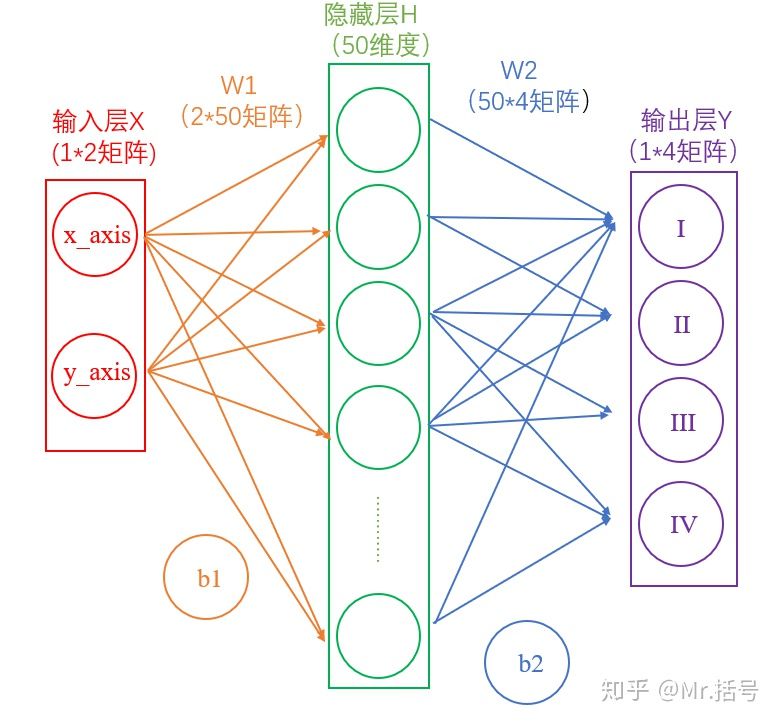
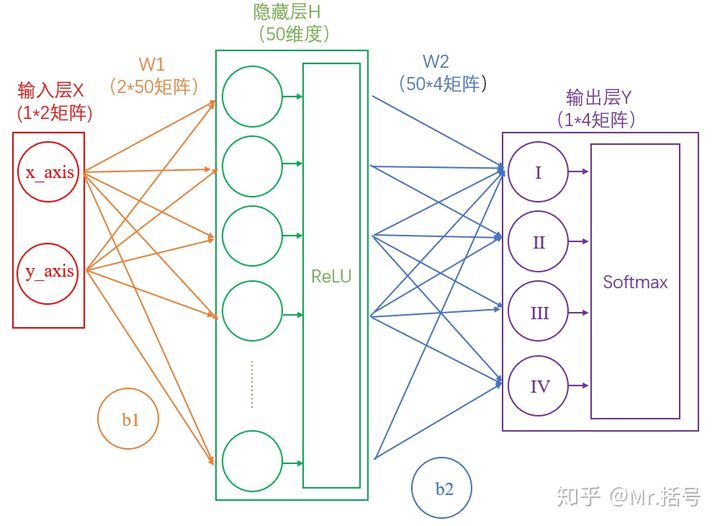
#### 1) 输入层
在我们的例子中,输入层是坐标值,例如$(1,1)$,这是一个包含两个元素的数组,也可以看作是一个$1\times 2$的矩阵。输入层的元素维度与输入量的特征息息相关,如果输入的是一张$32\times 32$像素的灰度图像,那么输入层的维度就是$32\times 32$。
#### 2) 隐藏层
连接输入层和隐藏层的是$W_1$和$b_1$。由X计算得到H十分简单,就是矩阵运算:
$$
H=X\cdot W_1+b_1
$$
如果你学过线性代数,对这个式子一定不陌生。如上图中所示,在设定隐藏层为50维(也可以理解成50个神经元)之后,矩阵H的大小为$1\times 50$的矩阵。
连接隐藏层和输出层的是W2和b2。同样是通过矩阵运算进行的:
$$
Y=H\cdot W_2+b_2
$$
**一系列线性方程的运算最终都可以用一个线性方程表示**
也就是说,上述两个式子联立后可以用一个线性方程表达。对于两次神经网络是这样,就算网络深度加到100层,也依然是这样。这样的话神经网络就失去了意义。
所以这里要对网络注入灵魂:**激活层**。
需要注意的是,每个隐藏层计算(矩阵线性运算)之后,都需要加一层激活层,要不然该层线性计算是没有意义的。
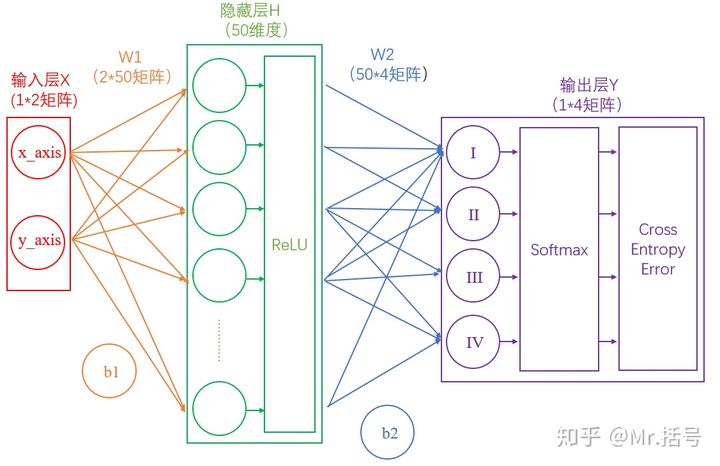
#### 3) 输出层
输出Y的值可能会是(3,1,0.1,0.5)这样的矩阵,诚然我们可以找到里边的最大值“3”,从而找到对应的分类为I,但是这并不直观。我们想让最终的输出为**概率**,也就是说可以生成像(90%,5%,2%,3%)这样的结果,这样做不仅可以找到最大概率的分类,而且可以知道各个分类计算的概率值。
具体是怎么计算的呢?
计算公式如下:
$S_i=\frac{e^i}{\sum_je^j}$
简单来说分三步进行:
(1)以e为底对所有元素求指数幂;
(2)将所有指数幂求和;
(3)分别将这些指数幂与该和做商。
这样求出的结果中,所有元素的和一定为1,而每个元素可以代表概率值。
我们将使用这个计算公式做输出结果正规化处理的层叫做“Softmax”层。此时的神经网络将变成
#### 4) Softmax-with-Loss 层
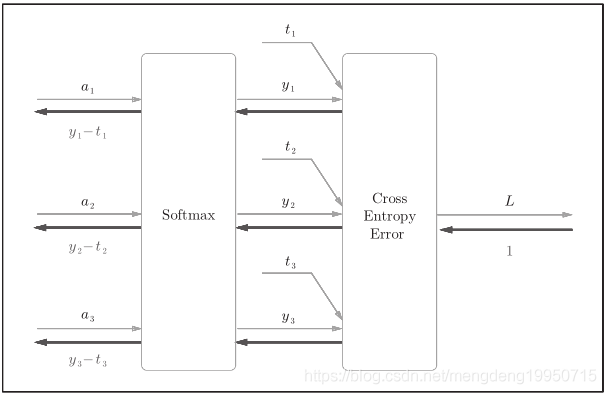
* Softmax层:将输入值正规化(输入值和调整为1,反映概率)后输出。
* Loss层:cross entropy error(交叉熵误差,一种损失函数)接收Softmax的输出(y1, y2, y3)和监督标签(t1, t2, t3), 输出损失L。
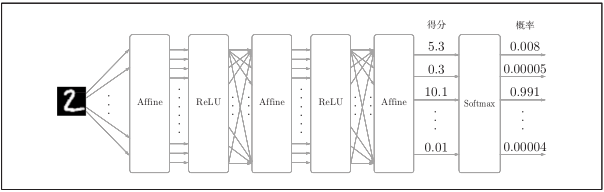
包含作为损失函数的交叉熵误差(cross entropy error),所以称为“Softmax-with-Loss层”。
Softmax-with-Loss层的计算图:
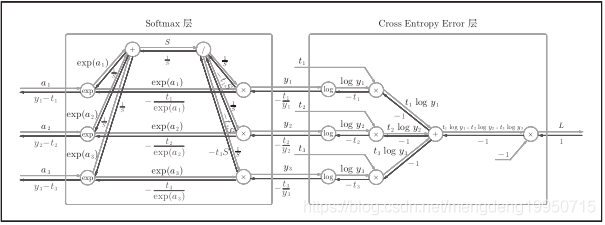
简易版Softmax-with-Loss层的计算图:
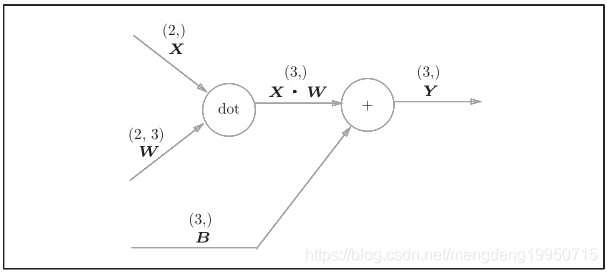
#### 5) Affine层
神经网络在传播时,进行的矩阵乘积运算。
神经网络的正向传播中,为了计算加权信号的总和,使用了矩阵的乘积运算(NumPy中是 np.dot())
神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”
如图:
## 2.3 损失函数
### 2.3.1 均方误差
$$
E=\frac{1}{2}\sum_{k}(y_k-t_k)^2
$$
$y_k$表示神经网络输出,$t_k$表示监督数据,k表示数据的维度
### 2.3.2 交叉熵误差
$$
E=-\sum_{k}t_klogy_k
$$
$y_k$表示神经网络输出,$t_k$表示监督数据,$k$表示数据的维度
$ log$是以e为底数的自然对数
参考文章
~~~bash
https://blog.csdn.net/qq_32790593/article/details/83619899
~~~
参考文章2
~~~bash
https://blog.csdn.net/qq_21966233/article/details/87189597
~~~
# 0. 概述
## 0.1 概念
很多人都有误解,以为深度学习比机器学习先进。其实深度学习是机器学习的一个分支。
可以理解为具有多层结构的模型。具体的话,深度学习是机器学习中的具有深层结构的神经网络算法,即机器学习>神经网络算法>深度神经网络(深度学习)。
深度学习(deep learning,以下简称DL),换种说法,可以说是基于人工神经网络的机器学习。区别于传统的机器学习,DL需要更多样本,换来更少的人工标注和更高的准确率。
传统的BP神经网络一般指三层的全连接神经网络,而大于三层就成了DNN(深度神经网络)。
事实上,DNN能解决一些问题,但因为参数太多,逐步被其他网络模型取代:CNN(卷积神经网络)、RNN(循环神经网络)。二者目前最成功的实现分别是ResNet和LSTM。
深度学习三巨头
* 神经网络之父**hinton**
* 卷积神经网络之父**lecun**
* GAN网络之父**bengio**
LSTM 之父 Jürgen Schmidhuber
## 0.2 历史
* 第一代`神经网络`又称为`感知器`,由科学家Frank Rosenblatt发明于1950至1960年代,它的算法只有两层,输入层输出层,,主要使用的是一种叫做sigmoid神经元(sigmoid neuron)的神经元模型,主要是线性结构。它不能解决线性不可分的问题,如异或操作。
* 为了解决第一代神经网络的缺陷,在`1980年左右`提出第二代神经网络`多层感知器(MLP)`。和第一代神经网络相比,第二代在输入输出层之间有增加了隐含层的感知机,引入一些非线性的结构,解决了之前无法模拟异或逻辑的缺陷。第二代神经网络让科学家们发现神经网络的层数直接决定了它对现实的表达能力,但是随着层数的增加,优化函数愈发容易出现局部最优解的现象,由于存在梯度消失的问题,深层网络往往难以训练,效果还不如浅层网络。
* 2006年`Hinton`采取无监督预训练(Pre-Training)的方法解决了梯度消失的问题,使得深度神经网络变得可训练,将隐含层发展到7层,有一个预训练的过程。使用微调技术作为反向传播和调优手段。减少了网络训练时间,并且提出了一个新的概念叫做"`深度学习`",直到2012年,在`ImageNet竞赛`中,`Hinton教授的团队`,使用以卷积神经网络为基础的深度学习方案,他们训练的模型面对15万张测试图像时,预测的头五个类别的错误率只有 15.3%,而排名第二的日本团队,使用的SVM方法构建的模型,相应的错误率则高达 26.2%。从此一战成名!2012年后深度学习就成为主流。
# 1. 感知机
资料参考
~~~bash
https://blog.csdn.net/m0_37957160/article/details/113922919
~~~
资料参考2
~~~bash
https://blog.csdn.net/Insincerity/article/details/106446689
~~~
资料参考3
~~~bash
https://www.jianshu.com/p/81fa7682daf3
~~~
## 1.1 概念
感知机是1957年,由Rosenblatt提出会,是**神经网络和支持向量机**的基础。
感知机是**二分类**的线性分类模型,输入为实例的特征向量,输出为实例的类别(取+1和-1)。感知机对应于输入空间中将**实例划分为两**类的分离超平面。感知机旨在求出该超平面,为求得超平面导入了基于误分类的损失函数,利用梯**度下降法对损失函数进行最优化**。

## 1.2 算法模型
### 1.2.1 模型
输入:$x\in R^n$,x是特征向量
输出:$Y\in \{-1,1\}$
由输入空间到输出空间的表达形式为:
$y=sign(w\times x+b)$
**上面该函数称为感知机,其中w,b称为模型的参数,$w\in R^n$称为权值,b称为偏置,$w\times x$表示为w,x的内积**
$$
f(n)=\begin{cases}1,if\quad n\ge 0\\ 0,otherwise\end{cases}
$$
下面是符号函数的函数图像(w为一维的数据量$w=[w_1]$):

### 1.2.2 分离超平面
感知机的作用就是找到一个分离超平面,使数据能够正确分为两类。
在实际情况中,w往往是$w=\begin{bmatrix}w_1\\ w_2\\ \vdots\\ w_n\end{bmatrix}$,多维的。这个时候$w\times x+b$表示的是超平面
在感知机中,一般把超平面方程写为:wx+b=0.
w 为超平面的法向量,b 是超平面的截距,超平面把数据分为两类,如下图。

### 1.2.3 损失函数
感知机能够自动地把 w 和 b 求解出来,求解过程中有个重点,就是**损失函数**的引入,损失函数也叫代价函数,是样本分类预测结果和样本实际类别差异的度量,正是通过最小化损失函数,感知机才能不断地修正w和b的值,找到一个最优的超平面。
1. 超平面的距离
感知机中的损失函数是所有误分类点到分离超平面的距离,其中,某一个误分类点到超平面的距离表示为:
$\frac{1}{||w||}|w\cdot x_0+b|$
$||w||$是$w$的$L_2$范数,这个**L2范数**乍听有点高大上,实际上就是 w 中每个元素去平方,然后相加开根号
$||w||=\sqrt{w_1^2+w_2^2+\dots+w_n^2}$
2. 误分类点到分离超平面的距离
对于一个误分类数据$(x_i,y_i)$,当 $w \cdot x_i + b > 0$ 时,$y_i =-1$;当$w\cdot x_i + b < 0$时,$y_i =1$;所以$y_i*(w\cdot x_i + b)>0$,所有误分类点到分离超平面的距离为:
$-\frac{1}{||w||}\sum_{x_i\in M}y_i(w\cdot x_i+b),M是误分类集合$
为啥距离是这个呢???,
$因为y_i=1或-1,不改变结果,只改变正负$
不考虑$\frac{1}{||w||}$损失函数写成这样:
$L(w,b)=-\sum_{x_i\in M}y_i(w\cdot x_i+b)$
我们的目标就是最小化损失函数 L(w,b),这里用 **随机梯度下降(SGD)**的方法来做最小化。
> L0范数是指向量中非0的元素的个数。(L0范数很难优化求解)
>
> L1范数是指向量中各个元素绝对值之和
>
> L2范数是指向量各元素的平方和然后求平方根
### 1.2.4 随机梯度下降
梯度下降方向就是梯度的反方向,最小化损失函数 L(w,b) 就是先求函数在 w 和 b 两个变量轴上的偏导:
$\nabla_wL(w,b)=-\sum_{x_i\in M}y_ix_i$
$\nabla_bL(w,b)=-\sum_{x_i\in M}y_i$
上面的式子,每更新一次参数,需要遍历整个数据集,如果数据集非常大的话,显然是不合适的,为了解决这个问题,只随机选取一个误分类点进行参数更新,这就是**随机梯度下降(SGD)**,如下所示。
$w+\eta y_ix_i\to w$
$b+\eta y_i\to b$
这里的 η 指的是**学习率**,相当于控制下山的步幅,$\eta$ 太小,函数拟合(收敛)过程会很慢,$\eta$太大,容易在最低点方向震荡,进入死循环。
当没有误分类点的时候,停止参数更新,所得的参数就是感知机学习的结果,这就是**感知机的原始形式**。下面总结一下参数更新的过程:
(1)预先设定一个$w_0$和$b_0$,即w和b的初值。
(2)在训练集中选取数据$(x_i,y_i)$。
(3)当$y_i*(w\cdot x_i +b)\le 0$时,利用随机梯度下降算法进行参数更新。
#### 例子
> 输入:正例$x_1=[3,3]^T,x_2=[4,3]^T,负例x_3=[1,1]^T。$
>
> 输出:感知机模型$f(x)=sign(w\times x+b)$
目标公式$min_{w,b}=-\sum_{x_i\in M}y_i(w\cdot x+b)$
* 假设$w_0=\begin{bmatrix}0&0\end{bmatrix},\eta=1,b_0=0$
* 判断$x_1$是否正确分类,$y_1(w_0\cdot x_1+b)=\begin{bmatrix}0&0\end{bmatrix}\begin{bmatrix}3\\ 3\end{bmatrix}+0=0$不能正确分类
更新$w,b$
* 更新公式为$w+\eta y_ix_i\to w$
$w_1=w_0+\eta y_1x_1=\begin{bmatrix}0&0\end{bmatrix}+1\times 1\times \begin{bmatrix}0&0\end{bmatrix}=\begin{bmatrix}3&3\end{bmatrix}$
同理$b_1=b_0+y_1=1$,得到新的模型$w_1\cdot x+b_1$
* 更新后的模型,对于$x_1,x_2$被正确分类,但是对于$x_3$错误分类。进行更新$w_1,b_1$
$w_2=w_1+\eta y_3x_3=\begin{bmatrix}0&0\end{bmatrix}+1\times (-1)\times \begin{bmatrix}1&1\end{bmatrix}=\begin{bmatrix}2&2\end{bmatrix}$$b_2=0$
依次类推
迭代过程如下
| 迭代次数 | 误分类点 | w | b | wx+b |
| -------- | -------- | --------------------------------- | ---- | ---- |
| 0 | | $\begin{bmatrix}0&0\end{bmatrix}$ | 0 | |
| 1 | $x_1$ | $\begin{bmatrix}3&3\end{bmatrix}$ | -1 | |
| 2 | $x_3$ | $\begin{bmatrix}2&2\end{bmatrix}$ | 0 | |
| 3 | $x_3$ | $\begin{bmatrix}1&1\end{bmatrix}$ | -1 | |
| 4 | $x_3$ | $\begin{bmatrix}0&0\end{bmatrix}$ | -2 | |
| 5 | $x_1$ | $\begin{bmatrix}3&3\end{bmatrix}$ | -1 | |
| 6 | $x_3$ | $\begin{bmatrix}2&2\end{bmatrix}$ | -2 | |
| 7 | $x_3$ | $\begin{bmatrix}1&1\end{bmatrix}$ | -3 | |
| 8 | 0 | $\begin{bmatrix}1&1\end{bmatrix}$ | -3 | |
### 1.2.5 对偶形式
将 w 和 b 表示为实例$x_1$和标记$y_1$线性组合的形式,通过求解系数来求解w和b,前面提到过这个式子:
$w+\eta y_ix_i\to w$
$b+\eta y_i\to b$
这里先假设 w 和 b 的初值为0,那么通过对偶形式能表示为什么?从上面式子可以看出来,每次迭代,w会增加一个 $ηy_ix_i$,b 会增加一个$ηy_i$,到最后参数更新完之后,w 和 b 一共增加了这些:
$w=\sum_{i=1}^N\alpha_iy_ix_i$
$b=\sum_{i=1}^N\alpha_iy_i$
这里的$α_i = n_i*η$,$n_i$就是$(x_i,y_i)$被误分类的次数,η 还是学习率。
$\alpha_i$越大,意味这实例点更新次数越多,距离分离超平面越近,越难被分类,对实例影响结果越大
下面是对偶形式的参数更新过程:
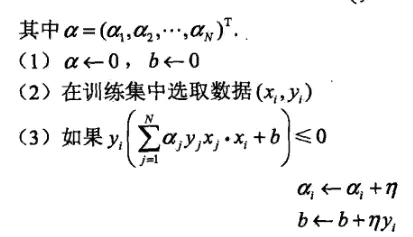
## 1.3 逻辑电路
### 1.3.1 与门
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
### 1.3.2 与非门
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
### 1.3.3 或门
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
### 1.3.4 异或门
什么是异或?就是,假如这里有两件事,一真一假,异或为真;两件事都为假或者两件事都为真,异或为假,就像这样:
0⊕0=0,0⊕1=1
1⊕0=1,1⊕1=0
下面是异或的函数图像:

通过图像可以看出,找不到一个超平面能将这四个点分隔开,所以**感知机无法处理异或问题,不仅仅是感知机,其他线性模型也无法处理这种问题。**
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
#### 多层感知机mlp
如何解决呢???
使用多层的感知机即可完成,如下图所示

与门、与非门、或门的符号
通过上面的感知机如何组成异或门呢??

这里,把$s_1$作为 与非门 的输出,把$s_2$ 作为或门的输出,填入真值表中。
结果如图所示,观察$x_1、x_2 、y$,可以发现确实符合异或门的输出

异或门是一种多层结构的神经网络。
与门、或门是单层感知机,而异或门是2层感知机。叠加了多 层的感知机也称为多层感知机(multi-layered perceptron) 。

**感知机的作用就是引出神经网络**
# 2. 神经网络
参考资料
~~~bash
https://blog.csdn.net/as091313/article/details/79080583
~~~
## 2.1 概念
### 2.1.1 概念
人工神经网络(artificial neural network,ANN),简称神经网络(neural network,NN),是一种模仿生物神经网络的结构和功能的数学模型或计算模型。
神经网络是一种**运算模型**,由大量的节点(或称“神经元”)和之间相互的联接构成。
每个节点代表一种特定的输出函数,称为**激励函数、激活函数**(activation function)。
每两个节点间的联接都代表一个对于通过该连接信号的加权值,称之为权重,这相当于人工神经网络的记忆。
网络的输出则依网络的连接方式,权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近,也可能是对一种逻辑策略的表达。
### 2.1.2 应用-分类
神经网络最重要的用途是分类,为了让大家对分类有个直观的认识,咱们先看几个例子:
* 垃圾邮件识别:现在有一封电子邮件,把出现在里面的所有词汇提取出来,送进一个机器里,机器需要判断这封邮件是否是垃圾邮件。
* 疾病判断:病人到医院去做了一大堆肝功、尿检测验,把测验结果送进一个机器里,机器需要判断这个病人是否得病,得的什么病。
* 猫狗分类:有一大堆猫、狗照片,把每一张照片送进一个机器里,机器需要判断这幅照片里的东西是猫还是狗。
## 2.2 前期准备
资料参考
~~~bash
https://zhuanlan.zhihu.com/p/65472471
~~~
### 2.2.1 神经元
神经网络中最基本的成分是神经元模型,即上述定义中的简单单元

> $Inputs$:输入
>
> $Weights$:权值,权重
>
> $Bias$:偏置,或者称为阈值
>
> $Activationfunction$:激活函数
>
> 这种“阈值加权和”的神经元模型称为**M-P模型** ( McCulloch-Pitts Model ),也称为神经网络的**一个处理单元**( PE, Processing Element )。
### 2.2.2 激活函数
参考资料
~~~bash
https://zhuanlan.zhihu.com/p/25279356
~~~
> 激活函数是用来加入非线性因素的,解决线性模型所不能解决的问题。
>
> 简而言之,激活层是为矩阵运算的结果添加非线性的。
常用的激活函数有三种,分别是阶跃函数、Sigmoid和ReLU。不要被奇怪的函数名吓到,其实它们的形式都很简单,如下图(更正:sigmoid在负无穷是应趋近于0):

* 阶跃函数:当输入小于等于0时,输出0;当输入大于0时,输出1。
* Sigmoid:当输入趋近于正无穷/负无穷时,输出无限接近于1/0。
* ReLU:当输入小于0时,输出0;当输入大于0时,输出等于输入。
#### 1) sigmoid函数
sigmoid函数是一种常见的挤压函数,其将较大范围的输入挤压到$(0,1)$区间内,其函数的表达式与形状如下图所示:

该函数常被用于分类模型,因为其具有很好的一个特性$f^\prime(x)=f(x)(1-f(x))$.这个函数也会被用于下面的神经网络模型中做激活函数。
#### 2) 双极性Sigmoid函数
$$
h(x)=\frac{2}{1+e^{-\alpha x}}-1
\\ h^\prime(x)=\frac{2\alpha e^{-\alpha x}}{(1+e^{-\alpha x})}=\alpha\frac{1-h(x)^2}{2}
$$
例子
$f(x)-\frac{1-e^{-x}}{1+e^{-x}}$

#### 3) 阶跃函数
阶跃函数是一种特殊的连续时间函数,是一个从0跳变到1的过程,属于奇异函数

####
#### 4) ReLU
**线性整流函数**(Rectified Linear Unit, **ReLU**),又称**修正线性单元,**是一种人工神经网络中常用的激活函数(activation function)

### 2.2.3 层介绍
该模型与一个有向无环图相关联
$f(x)=f^{(3)}(f^{(2)}(f^{(1)}(x)))$
$f^{(1)}$被称为网络的第一层,叫做输入层
$f^{(2)}$被称为网络的第二层,叫做隐藏层
$f^{(3)}$被称为网络的第三层,叫做输出层

#### 1) 输入层
在我们的例子中,输入层是坐标值,例如$(1,1)$,这是一个包含两个元素的数组,也可以看作是一个$1\times 2$的矩阵。输入层的元素维度与输入量的特征息息相关,如果输入的是一张$32\times 32$像素的灰度图像,那么输入层的维度就是$32\times 32$。
#### 2) 隐藏层
连接输入层和隐藏层的是$W_1$和$b_1$。由X计算得到H十分简单,就是矩阵运算:
$$
H=X\cdot W_1+b_1
$$
如果你学过线性代数,对这个式子一定不陌生。如上图中所示,在设定隐藏层为50维(也可以理解成50个神经元)之后,矩阵H的大小为$1\times 50$的矩阵。
连接隐藏层和输出层的是W2和b2。同样是通过矩阵运算进行的:
$$
Y=H\cdot W_2+b_2
$$
**一系列线性方程的运算最终都可以用一个线性方程表示**
也就是说,上述两个式子联立后可以用一个线性方程表达。对于两次神经网络是这样,就算网络深度加到100层,也依然是这样。这样的话神经网络就失去了意义。
所以这里要对网络注入灵魂:**激活层**。
需要注意的是,每个隐藏层计算(矩阵线性运算)之后,都需要加一层激活层,要不然该层线性计算是没有意义的。

#### 3) 输出层
输出Y的值可能会是(3,1,0.1,0.5)这样的矩阵,诚然我们可以找到里边的最大值“3”,从而找到对应的分类为I,但是这并不直观。我们想让最终的输出为**概率**,也就是说可以生成像(90%,5%,2%,3%)这样的结果,这样做不仅可以找到最大概率的分类,而且可以知道各个分类计算的概率值。
具体是怎么计算的呢?
计算公式如下:
$S_i=\frac{e^i}{\sum_je^j}$
简单来说分三步进行:
(1)以e为底对所有元素求指数幂;
(2)将所有指数幂求和;
(3)分别将这些指数幂与该和做商。
这样求出的结果中,所有元素的和一定为1,而每个元素可以代表概率值。
我们将使用这个计算公式做输出结果正规化处理的层叫做“Softmax”层。此时的神经网络将变成

#### 4) Softmax-with-Loss 层
* Softmax层:将输入值正规化(输入值和调整为1,反映概率)后输出。
* Loss层:cross entropy error(交叉熵误差,一种损失函数)接收Softmax的输出(y1, y2, y3)和监督标签(t1, t2, t3), 输出损失L。

包含作为损失函数的交叉熵误差(cross entropy error),所以称为“Softmax-with-Loss层”。
Softmax-with-Loss层的计算图:

简易版Softmax-with-Loss层的计算图:

#### 5) Affine层
神经网络在传播时,进行的矩阵乘积运算。
神经网络的正向传播中,为了计算加权信号的总和,使用了矩阵的乘积运算(NumPy中是 np.dot())
神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”
如图:

## 2.3 损失函数
### 2.3.1 均方误差
$$
E=\frac{1}{2}\sum_{k}(y_k-t_k)^2
$$
$y_k$表示神经网络输出,$t_k$表示监督数据,k表示数据的维度
### 2.3.2 交叉熵误差
$$
E=-\sum_{k}t_klogy_k
$$
$y_k$表示神经网络输出,$t_k$表示监督数据,$k$表示数据的维度
$ log$是以e为底数的自然对数
参考文章
~~~bash
https://blog.csdn.net/qq_32790593/article/details/83619899
~~~
参考文章2
~~~bash
https://blog.csdn.net/qq_21966233/article/details/87189597
~~~ # 0. 概述
## 0.1 概念
很多人都有误解,以为深度学习比机器学习先进。其实深度学习是机器学习的一个分支。
可以理解为具有多层结构的模型。具体的话,深度学习是机器学习中的具有深层结构的神经网络算法,即机器学习>神经网络算法>深度神经网络(深度学习)。
深度学习(deep learning,以下简称DL),换种说法,可以说是基于人工神经网络的机器学习。区别于传统的机器学习,DL需要更多样本,换来更少的人工标注和更高的准确率。
传统的BP神经网络一般指三层的全连接神经网络,而大于三层就成了DNN(深度神经网络)。
事实上,DNN能解决一些问题,但因为参数太多,逐步被其他网络模型取代:CNN(卷积神经网络)、RNN(循环神经网络)。二者目前最成功的实现分别是ResNet和LSTM。
深度学习三巨头
* 神经网络之父**hinton**
* 卷积神经网络之父**lecun**
* GAN网络之父**bengio**
LSTM 之父 Jürgen Schmidhuber
## 0.2 历史
* 第一代`神经网络`又称为`感知器`,由科学家Frank Rosenblatt发明于1950至1960年代,它的算法只有两层,输入层输出层,,主要使用的是一种叫做sigmoid神经元(sigmoid neuron)的神经元模型,主要是线性结构。它不能解决线性不可分的问题,如异或操作。
* 为了解决第一代神经网络的缺陷,在`1980年左右`提出第二代神经网络`多层感知器(MLP)`。和第一代神经网络相比,第二代在输入输出层之间有增加了隐含层的感知机,引入一些非线性的结构,解决了之前无法模拟异或逻辑的缺陷。第二代神经网络让科学家们发现神经网络的层数直接决定了它对现实的表达能力,但是随着层数的增加,优化函数愈发容易出现局部最优解的现象,由于存在梯度消失的问题,深层网络往往难以训练,效果还不如浅层网络。
* 2006年`Hinton`采取无监督预训练(Pre-Training)的方法解决了梯度消失的问题,使得深度神经网络变得可训练,将隐含层发展到7层,有一个预训练的过程。使用微调技术作为反向传播和调优手段。减少了网络训练时间,并且提出了一个新的概念叫做"`深度学习`",直到2012年,在`ImageNet竞赛`中,`Hinton教授的团队`,使用以卷积神经网络为基础的深度学习方案,他们训练的模型面对15万张测试图像时,预测的头五个类别的错误率只有 15.3%,而排名第二的日本团队,使用的SVM方法构建的模型,相应的错误率则高达 26.2%。从此一战成名!2012年后深度学习就成为主流。
# 1. 感知机
资料参考
~~~bash
https://blog.csdn.net/m0_37957160/article/details/113922919
~~~
资料参考2
~~~bash
https://blog.csdn.net/Insincerity/article/details/106446689
~~~
资料参考3
~~~bash
https://www.jianshu.com/p/81fa7682daf3
~~~
## 1.1 概念
感知机是1957年,由Rosenblatt提出会,是**神经网络和支持向量机**的基础。
感知机是**二分类**的线性分类模型,输入为实例的特征向量,输出为实例的类别(取+1和-1)。感知机对应于输入空间中将**实例划分为两**类的分离超平面。感知机旨在求出该超平面,为求得超平面导入了基于误分类的损失函数,利用梯**度下降法对损失函数进行最优化**。

## 1.2 算法模型
### 1.2.1 模型
输入:$x\in R^n$,x是特征向量
输出:$Y\in \{-1,1\}$
由输入空间到输出空间的表达形式为:
$y=sign(w\times x+b)$
**上面该函数称为感知机,其中w,b称为模型的参数,$w\in R^n$称为权值,b称为偏置,$w\times x$表示为w,x的内积**
$$
f(n)=\begin{cases}1,if\quad n\ge 0\\ 0,otherwise\end{cases}
$$
下面是符号函数的函数图像(w为一维的数据量$w=[w_1]$):

### 1.2.2 分离超平面
感知机的作用就是找到一个分离超平面,使数据能够正确分为两类。
在实际情况中,w往往是$w=\begin{bmatrix}w_1\\ w_2\\ \vdots\\ w_n\end{bmatrix}$,多维的。这个时候$w\times x+b$表示的是超平面
在感知机中,一般把超平面方程写为:wx+b=0.
w 为超平面的法向量,b 是超平面的截距,超平面把数据分为两类,如下图。

### 1.2.3 损失函数
感知机能够自动地把 w 和 b 求解出来,求解过程中有个重点,就是**损失函数**的引入,损失函数也叫代价函数,是样本分类预测结果和样本实际类别差异的度量,正是通过最小化损失函数,感知机才能不断地修正w和b的值,找到一个最优的超平面。
1. 超平面的距离
感知机中的损失函数是所有误分类点到分离超平面的距离,其中,某一个误分类点到超平面的距离表示为:
$\frac{1}{||w||}|w\cdot x_0+b|$
$||w||$是$w$的$L_2$范数,这个**L2范数**乍听有点高大上,实际上就是 w 中每个元素去平方,然后相加开根号
$||w||=\sqrt{w_1^2+w_2^2+\dots+w_n^2}$
2. 误分类点到分离超平面的距离
对于一个误分类数据$(x_i,y_i)$,当 $w \cdot x_i + b > 0$ 时,$y_i =-1$;当$w\cdot x_i + b < 0$时,$y_i =1$;所以$y_i*(w\cdot x_i + b)>0$,所有误分类点到分离超平面的距离为:
$-\frac{1}{||w||}\sum_{x_i\in M}y_i(w\cdot x_i+b),M是误分类集合$
为啥距离是这个呢???,
$因为y_i=1或-1,不改变结果,只改变正负$
不考虑$\frac{1}{||w||}$损失函数写成这样:
$L(w,b)=-\sum_{x_i\in M}y_i(w\cdot x_i+b)$
我们的目标就是最小化损失函数 L(w,b),这里用 **随机梯度下降(SGD)**的方法来做最小化。
> L0范数是指向量中非0的元素的个数。(L0范数很难优化求解)
>
> L1范数是指向量中各个元素绝对值之和
>
> L2范数是指向量各元素的平方和然后求平方根
### 1.2.4 随机梯度下降
梯度下降方向就是梯度的反方向,最小化损失函数 L(w,b) 就是先求函数在 w 和 b 两个变量轴上的偏导:
$\nabla_wL(w,b)=-\sum_{x_i\in M}y_ix_i$
$\nabla_bL(w,b)=-\sum_{x_i\in M}y_i$
上面的式子,每更新一次参数,需要遍历整个数据集,如果数据集非常大的话,显然是不合适的,为了解决这个问题,只随机选取一个误分类点进行参数更新,这就是**随机梯度下降(SGD)**,如下所示。
$w+\eta y_ix_i\to w$
$b+\eta y_i\to b$
这里的 η 指的是**学习率**,相当于控制下山的步幅,$\eta$ 太小,函数拟合(收敛)过程会很慢,$\eta$太大,容易在最低点方向震荡,进入死循环。
当没有误分类点的时候,停止参数更新,所得的参数就是感知机学习的结果,这就是**感知机的原始形式**。下面总结一下参数更新的过程:
(1)预先设定一个$w_0$和$b_0$,即w和b的初值。
(2)在训练集中选取数据$(x_i,y_i)$。
(3)当$y_i*(w\cdot x_i +b)\le 0$时,利用随机梯度下降算法进行参数更新。
#### 例子
> 输入:正例$x_1=[3,3]^T,x_2=[4,3]^T,负例x_3=[1,1]^T。$
>
> 输出:感知机模型$f(x)=sign(w\times x+b)$
目标公式$min_{w,b}=-\sum_{x_i\in M}y_i(w\cdot x+b)$
* 假设$w_0=\begin{bmatrix}0&0\end{bmatrix},\eta=1,b_0=0$
* 判断$x_1$是否正确分类,$y_1(w_0\cdot x_1+b)=\begin{bmatrix}0&0\end{bmatrix}\begin{bmatrix}3\\ 3\end{bmatrix}+0=0$不能正确分类
更新$w,b$
* 更新公式为$w+\eta y_ix_i\to w$
$w_1=w_0+\eta y_1x_1=\begin{bmatrix}0&0\end{bmatrix}+1\times 1\times \begin{bmatrix}0&0\end{bmatrix}=\begin{bmatrix}3&3\end{bmatrix}$
同理$b_1=b_0+y_1=1$,得到新的模型$w_1\cdot x+b_1$
* 更新后的模型,对于$x_1,x_2$被正确分类,但是对于$x_3$错误分类。进行更新$w_1,b_1$
$w_2=w_1+\eta y_3x_3=\begin{bmatrix}0&0\end{bmatrix}+1\times (-1)\times \begin{bmatrix}1&1\end{bmatrix}=\begin{bmatrix}2&2\end{bmatrix}$$b_2=0$
依次类推
迭代过程如下
| 迭代次数 | 误分类点 | w | b | wx+b |
| -------- | -------- | --------------------------------- | ---- | ---- |
| 0 | | $\begin{bmatrix}0&0\end{bmatrix}$ | 0 | |
| 1 | $x_1$ | $\begin{bmatrix}3&3\end{bmatrix}$ | -1 | |
| 2 | $x_3$ | $\begin{bmatrix}2&2\end{bmatrix}$ | 0 | |
| 3 | $x_3$ | $\begin{bmatrix}1&1\end{bmatrix}$ | -1 | |
| 4 | $x_3$ | $\begin{bmatrix}0&0\end{bmatrix}$ | -2 | |
| 5 | $x_1$ | $\begin{bmatrix}3&3\end{bmatrix}$ | -1 | |
| 6 | $x_3$ | $\begin{bmatrix}2&2\end{bmatrix}$ | -2 | |
| 7 | $x_3$ | $\begin{bmatrix}1&1\end{bmatrix}$ | -3 | |
| 8 | 0 | $\begin{bmatrix}1&1\end{bmatrix}$ | -3 | |
### 1.2.5 对偶形式
将 w 和 b 表示为实例$x_1$和标记$y_1$线性组合的形式,通过求解系数来求解w和b,前面提到过这个式子:
$w+\eta y_ix_i\to w$
$b+\eta y_i\to b$
这里先假设 w 和 b 的初值为0,那么通过对偶形式能表示为什么?从上面式子可以看出来,每次迭代,w会增加一个 $ηy_ix_i$,b 会增加一个$ηy_i$,到最后参数更新完之后,w 和 b 一共增加了这些:
$w=\sum_{i=1}^N\alpha_iy_ix_i$
$b=\sum_{i=1}^N\alpha_iy_i$
这里的$α_i = n_i*η$,$n_i$就是$(x_i,y_i)$被误分类的次数,η 还是学习率。
$\alpha_i$越大,意味这实例点更新次数越多,距离分离超平面越近,越难被分类,对实例影响结果越大
下面是对偶形式的参数更新过程:
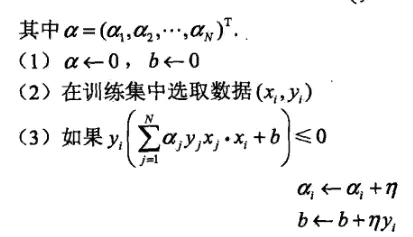
## 1.3 逻辑电路
### 1.3.1 与门
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
### 1.3.2 与非门
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
### 1.3.3 或门
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
### 1.3.4 异或门
什么是异或?就是,假如这里有两件事,一真一假,异或为真;两件事都为假或者两件事都为真,异或为假,就像这样:
0⊕0=0,0⊕1=1
1⊕0=1,1⊕1=0
下面是异或的函数图像:

通过图像可以看出,找不到一个超平面能将这四个点分隔开,所以**感知机无法处理异或问题,不仅仅是感知机,其他线性模型也无法处理这种问题。**
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
#### 多层感知机mlp
如何解决呢???
使用多层的感知机即可完成,如下图所示

与门、与非门、或门的符号
通过上面的感知机如何组成异或门呢??

这里,把$s_1$作为 与非门 的输出,把$s_2$ 作为或门的输出,填入真值表中。
结果如图所示,观察$x_1、x_2 、y$,可以发现确实符合异或门的输出

异或门是一种多层结构的神经网络。
与门、或门是单层感知机,而异或门是2层感知机。叠加了多 层的感知机也称为多层感知机(multi-layered perceptron) 。

**感知机的作用就是引出神经网络**
# 2. 神经网络
参考资料
~~~bash
https://blog.csdn.net/as091313/article/details/79080583
~~~
## 2.1 概念
### 2.1.1 概念
人工神经网络(artificial neural network,ANN),简称神经网络(neural network,NN),是一种模仿生物神经网络的结构和功能的数学模型或计算模型。
神经网络是一种**运算模型**,由大量的节点(或称“神经元”)和之间相互的联接构成。
每个节点代表一种特定的输出函数,称为**激励函数、激活函数**(activation function)。
每两个节点间的联接都代表一个对于通过该连接信号的加权值,称之为权重,这相当于人工神经网络的记忆。
网络的输出则依网络的连接方式,权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近,也可能是对一种逻辑策略的表达。
### 2.1.2 应用-分类
神经网络最重要的用途是分类,为了让大家对分类有个直观的认识,咱们先看几个例子:
* 垃圾邮件识别:现在有一封电子邮件,把出现在里面的所有词汇提取出来,送进一个机器里,机器需要判断这封邮件是否是垃圾邮件。
* 疾病判断:病人到医院去做了一大堆肝功、尿检测验,把测验结果送进一个机器里,机器需要判断这个病人是否得病,得的什么病。
* 猫狗分类:有一大堆猫、狗照片,把每一张照片送进一个机器里,机器需要判断这幅照片里的东西是猫还是狗。
## 2.2 前期准备
资料参考
~~~bash
https://zhuanlan.zhihu.com/p/65472471
~~~
### 2.2.1 神经元
神经网络中最基本的成分是神经元模型,即上述定义中的简单单元

> $Inputs$:输入
>
> $Weights$:权值,权重
>
> $Bias$:偏置,或者称为阈值
>
> $Activationfunction$:激活函数
>
> 这种“阈值加权和”的神经元模型称为**M-P模型** ( McCulloch-Pitts Model ),也称为神经网络的**一个处理单元**( PE, Processing Element )。
### 2.2.2 激活函数
参考资料
~~~bash
https://zhuanlan.zhihu.com/p/25279356
~~~
> 激活函数是用来加入非线性因素的,解决线性模型所不能解决的问题。
>
> 简而言之,激活层是为矩阵运算的结果添加非线性的。
常用的激活函数有三种,分别是阶跃函数、Sigmoid和ReLU。不要被奇怪的函数名吓到,其实它们的形式都很简单,如下图(更正:sigmoid在负无穷是应趋近于0):

* 阶跃函数:当输入小于等于0时,输出0;当输入大于0时,输出1。
* Sigmoid:当输入趋近于正无穷/负无穷时,输出无限接近于1/0。
* ReLU:当输入小于0时,输出0;当输入大于0时,输出等于输入。
#### 1) sigmoid函数
sigmoid函数是一种常见的挤压函数,其将较大范围的输入挤压到$(0,1)$区间内,其函数的表达式与形状如下图所示:

该函数常被用于分类模型,因为其具有很好的一个特性$f^\prime(x)=f(x)(1-f(x))$.这个函数也会被用于下面的神经网络模型中做激活函数。
#### 2) 双极性Sigmoid函数
$$
h(x)=\frac{2}{1+e^{-\alpha x}}-1
\\ h^\prime(x)=\frac{2\alpha e^{-\alpha x}}{(1+e^{-\alpha x})}=\alpha\frac{1-h(x)^2}{2}
$$
例子
$f(x)-\frac{1-e^{-x}}{1+e^{-x}}$

#### 3) 阶跃函数
阶跃函数是一种特殊的连续时间函数,是一个从0跳变到1的过程,属于奇异函数

####
#### 4) ReLU
**线性整流函数**(Rectified Linear Unit, **ReLU**),又称**修正线性单元,**是一种人工神经网络中常用的激活函数(activation function)

### 2.2.3 层介绍
该模型与一个有向无环图相关联
$f(x)=f^{(3)}(f^{(2)}(f^{(1)}(x)))$
$f^{(1)}$被称为网络的第一层,叫做输入层
$f^{(2)}$被称为网络的第二层,叫做隐藏层
$f^{(3)}$被称为网络的第三层,叫做输出层

#### 1) 输入层
在我们的例子中,输入层是坐标值,例如$(1,1)$,这是一个包含两个元素的数组,也可以看作是一个$1\times 2$的矩阵。输入层的元素维度与输入量的特征息息相关,如果输入的是一张$32\times 32$像素的灰度图像,那么输入层的维度就是$32\times 32$。
#### 2) 隐藏层
连接输入层和隐藏层的是$W_1$和$b_1$。由X计算得到H十分简单,就是矩阵运算:
$$
H=X\cdot W_1+b_1
$$
如果你学过线性代数,对这个式子一定不陌生。如上图中所示,在设定隐藏层为50维(也可以理解成50个神经元)之后,矩阵H的大小为$1\times 50$的矩阵。
连接隐藏层和输出层的是W2和b2。同样是通过矩阵运算进行的:
$$
Y=H\cdot W_2+b_2
$$
**一系列线性方程的运算最终都可以用一个线性方程表示**
也就是说,上述两个式子联立后可以用一个线性方程表达。对于两次神经网络是这样,就算网络深度加到100层,也依然是这样。这样的话神经网络就失去了意义。
所以这里要对网络注入灵魂:**激活层**。
需要注意的是,每个隐藏层计算(矩阵线性运算)之后,都需要加一层激活层,要不然该层线性计算是没有意义的。

#### 3) 输出层
输出Y的值可能会是(3,1,0.1,0.5)这样的矩阵,诚然我们可以找到里边的最大值“3”,从而找到对应的分类为I,但是这并不直观。我们想让最终的输出为**概率**,也就是说可以生成像(90%,5%,2%,3%)这样的结果,这样做不仅可以找到最大概率的分类,而且可以知道各个分类计算的概率值。
具体是怎么计算的呢?
计算公式如下:
$S_i=\frac{e^i}{\sum_je^j}$
简单来说分三步进行:
(1)以e为底对所有元素求指数幂;
(2)将所有指数幂求和;
(3)分别将这些指数幂与该和做商。
这样求出的结果中,所有元素的和一定为1,而每个元素可以代表概率值。
我们将使用这个计算公式做输出结果正规化处理的层叫做“Softmax”层。此时的神经网络将变成

#### 4) Softmax-with-Loss 层
* Softmax层:将输入值正规化(输入值和调整为1,反映概率)后输出。
* Loss层:cross entropy error(交叉熵误差,一种损失函数)接收Softmax的输出(y1, y2, y3)和监督标签(t1, t2, t3), 输出损失L。

包含作为损失函数的交叉熵误差(cross entropy error),所以称为“Softmax-with-Loss层”。
Softmax-with-Loss层的计算图:

简易版Softmax-with-Loss层的计算图:

#### 5) Affine层
神经网络在传播时,进行的矩阵乘积运算。
神经网络的正向传播中,为了计算加权信号的总和,使用了矩阵的乘积运算(NumPy中是 np.dot())
神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”
如图:

## 2.3 损失函数
### 2.3.1 均方误差
$$
E=\frac{1}{2}\sum_{k}(y_k-t_k)^2
$$
$y_k$表示神经网络输出,$t_k$表示监督数据,k表示数据的维度
### 2.3.2 交叉熵误差
$$
E=-\sum_{k}t_klogy_k
$$
$y_k$表示神经网络输出,$t_k$表示监督数据,$k$表示数据的维度
$ log$是以e为底数的自然对数
参考文章
~~~bash
https://blog.csdn.net/qq_32790593/article/details/83619899
~~~
参考文章2
~~~bash
https://blog.csdn.net/qq_21966233/article/details/87189597
~~~
# 0. 概述
## 0.1 概念
很多人都有误解,以为深度学习比机器学习先进。其实深度学习是机器学习的一个分支。
可以理解为具有多层结构的模型。具体的话,深度学习是机器学习中的具有深层结构的神经网络算法,即机器学习>神经网络算法>深度神经网络(深度学习)。
深度学习(deep learning,以下简称DL),换种说法,可以说是基于人工神经网络的机器学习。区别于传统的机器学习,DL需要更多样本,换来更少的人工标注和更高的准确率。
传统的BP神经网络一般指三层的全连接神经网络,而大于三层就成了DNN(深度神经网络)。
事实上,DNN能解决一些问题,但因为参数太多,逐步被其他网络模型取代:CNN(卷积神经网络)、RNN(循环神经网络)。二者目前最成功的实现分别是ResNet和LSTM。
深度学习三巨头
* 神经网络之父**hinton**
* 卷积神经网络之父**lecun**
* GAN网络之父**bengio**
LSTM 之父 Jürgen Schmidhuber
## 0.2 历史
* 第一代`神经网络`又称为`感知器`,由科学家Frank Rosenblatt发明于1950至1960年代,它的算法只有两层,输入层输出层,,主要使用的是一种叫做sigmoid神经元(sigmoid neuron)的神经元模型,主要是线性结构。它不能解决线性不可分的问题,如异或操作。
* 为了解决第一代神经网络的缺陷,在`1980年左右`提出第二代神经网络`多层感知器(MLP)`。和第一代神经网络相比,第二代在输入输出层之间有增加了隐含层的感知机,引入一些非线性的结构,解决了之前无法模拟异或逻辑的缺陷。第二代神经网络让科学家们发现神经网络的层数直接决定了它对现实的表达能力,但是随着层数的增加,优化函数愈发容易出现局部最优解的现象,由于存在梯度消失的问题,深层网络往往难以训练,效果还不如浅层网络。
* 2006年`Hinton`采取无监督预训练(Pre-Training)的方法解决了梯度消失的问题,使得深度神经网络变得可训练,将隐含层发展到7层,有一个预训练的过程。使用微调技术作为反向传播和调优手段。减少了网络训练时间,并且提出了一个新的概念叫做"`深度学习`",直到2012年,在`ImageNet竞赛`中,`Hinton教授的团队`,使用以卷积神经网络为基础的深度学习方案,他们训练的模型面对15万张测试图像时,预测的头五个类别的错误率只有 15.3%,而排名第二的日本团队,使用的SVM方法构建的模型,相应的错误率则高达 26.2%。从此一战成名!2012年后深度学习就成为主流。
# 1. 感知机
资料参考
~~~bash
https://blog.csdn.net/m0_37957160/article/details/113922919
~~~
资料参考2
~~~bash
https://blog.csdn.net/Insincerity/article/details/106446689
~~~
资料参考3
~~~bash
https://www.jianshu.com/p/81fa7682daf3
~~~
## 1.1 概念
感知机是1957年,由Rosenblatt提出会,是**神经网络和支持向量机**的基础。
感知机是**二分类**的线性分类模型,输入为实例的特征向量,输出为实例的类别(取+1和-1)。感知机对应于输入空间中将**实例划分为两**类的分离超平面。感知机旨在求出该超平面,为求得超平面导入了基于误分类的损失函数,利用梯**度下降法对损失函数进行最优化**。

## 1.2 算法模型
### 1.2.1 模型
输入:$x\in R^n$,x是特征向量
输出:$Y\in \{-1,1\}$
由输入空间到输出空间的表达形式为:
$y=sign(w\times x+b)$
**上面该函数称为感知机,其中w,b称为模型的参数,$w\in R^n$称为权值,b称为偏置,$w\times x$表示为w,x的内积**
$$
f(n)=\begin{cases}1,if\quad n\ge 0\\ 0,otherwise\end{cases}
$$
下面是符号函数的函数图像(w为一维的数据量$w=[w_1]$):

### 1.2.2 分离超平面
感知机的作用就是找到一个分离超平面,使数据能够正确分为两类。
在实际情况中,w往往是$w=\begin{bmatrix}w_1\\ w_2\\ \vdots\\ w_n\end{bmatrix}$,多维的。这个时候$w\times x+b$表示的是超平面
在感知机中,一般把超平面方程写为:wx+b=0.
w 为超平面的法向量,b 是超平面的截距,超平面把数据分为两类,如下图。

### 1.2.3 损失函数
感知机能够自动地把 w 和 b 求解出来,求解过程中有个重点,就是**损失函数**的引入,损失函数也叫代价函数,是样本分类预测结果和样本实际类别差异的度量,正是通过最小化损失函数,感知机才能不断地修正w和b的值,找到一个最优的超平面。
1. 超平面的距离
感知机中的损失函数是所有误分类点到分离超平面的距离,其中,某一个误分类点到超平面的距离表示为:
$\frac{1}{||w||}|w\cdot x_0+b|$
$||w||$是$w$的$L_2$范数,这个**L2范数**乍听有点高大上,实际上就是 w 中每个元素去平方,然后相加开根号
$||w||=\sqrt{w_1^2+w_2^2+\dots+w_n^2}$
2. 误分类点到分离超平面的距离
对于一个误分类数据$(x_i,y_i)$,当 $w \cdot x_i + b > 0$ 时,$y_i =-1$;当$w\cdot x_i + b < 0$时,$y_i =1$;所以$y_i*(w\cdot x_i + b)>0$,所有误分类点到分离超平面的距离为:
$-\frac{1}{||w||}\sum_{x_i\in M}y_i(w\cdot x_i+b),M是误分类集合$
为啥距离是这个呢???,
$因为y_i=1或-1,不改变结果,只改变正负$
不考虑$\frac{1}{||w||}$损失函数写成这样:
$L(w,b)=-\sum_{x_i\in M}y_i(w\cdot x_i+b)$
我们的目标就是最小化损失函数 L(w,b),这里用 **随机梯度下降(SGD)**的方法来做最小化。
> L0范数是指向量中非0的元素的个数。(L0范数很难优化求解)
>
> L1范数是指向量中各个元素绝对值之和
>
> L2范数是指向量各元素的平方和然后求平方根
### 1.2.4 随机梯度下降
梯度下降方向就是梯度的反方向,最小化损失函数 L(w,b) 就是先求函数在 w 和 b 两个变量轴上的偏导:
$\nabla_wL(w,b)=-\sum_{x_i\in M}y_ix_i$
$\nabla_bL(w,b)=-\sum_{x_i\in M}y_i$
上面的式子,每更新一次参数,需要遍历整个数据集,如果数据集非常大的话,显然是不合适的,为了解决这个问题,只随机选取一个误分类点进行参数更新,这就是**随机梯度下降(SGD)**,如下所示。
$w+\eta y_ix_i\to w$
$b+\eta y_i\to b$
这里的 η 指的是**学习率**,相当于控制下山的步幅,$\eta$ 太小,函数拟合(收敛)过程会很慢,$\eta$太大,容易在最低点方向震荡,进入死循环。
当没有误分类点的时候,停止参数更新,所得的参数就是感知机学习的结果,这就是**感知机的原始形式**。下面总结一下参数更新的过程:
(1)预先设定一个$w_0$和$b_0$,即w和b的初值。
(2)在训练集中选取数据$(x_i,y_i)$。
(3)当$y_i*(w\cdot x_i +b)\le 0$时,利用随机梯度下降算法进行参数更新。
#### 例子
> 输入:正例$x_1=[3,3]^T,x_2=[4,3]^T,负例x_3=[1,1]^T。$
>
> 输出:感知机模型$f(x)=sign(w\times x+b)$
目标公式$min_{w,b}=-\sum_{x_i\in M}y_i(w\cdot x+b)$
* 假设$w_0=\begin{bmatrix}0&0\end{bmatrix},\eta=1,b_0=0$
* 判断$x_1$是否正确分类,$y_1(w_0\cdot x_1+b)=\begin{bmatrix}0&0\end{bmatrix}\begin{bmatrix}3\\ 3\end{bmatrix}+0=0$不能正确分类
更新$w,b$
* 更新公式为$w+\eta y_ix_i\to w$
$w_1=w_0+\eta y_1x_1=\begin{bmatrix}0&0\end{bmatrix}+1\times 1\times \begin{bmatrix}0&0\end{bmatrix}=\begin{bmatrix}3&3\end{bmatrix}$
同理$b_1=b_0+y_1=1$,得到新的模型$w_1\cdot x+b_1$
* 更新后的模型,对于$x_1,x_2$被正确分类,但是对于$x_3$错误分类。进行更新$w_1,b_1$
$w_2=w_1+\eta y_3x_3=\begin{bmatrix}0&0\end{bmatrix}+1\times (-1)\times \begin{bmatrix}1&1\end{bmatrix}=\begin{bmatrix}2&2\end{bmatrix}$$b_2=0$
依次类推
迭代过程如下
| 迭代次数 | 误分类点 | w | b | wx+b |
| -------- | -------- | --------------------------------- | ---- | ---- |
| 0 | | $\begin{bmatrix}0&0\end{bmatrix}$ | 0 | |
| 1 | $x_1$ | $\begin{bmatrix}3&3\end{bmatrix}$ | -1 | |
| 2 | $x_3$ | $\begin{bmatrix}2&2\end{bmatrix}$ | 0 | |
| 3 | $x_3$ | $\begin{bmatrix}1&1\end{bmatrix}$ | -1 | |
| 4 | $x_3$ | $\begin{bmatrix}0&0\end{bmatrix}$ | -2 | |
| 5 | $x_1$ | $\begin{bmatrix}3&3\end{bmatrix}$ | -1 | |
| 6 | $x_3$ | $\begin{bmatrix}2&2\end{bmatrix}$ | -2 | |
| 7 | $x_3$ | $\begin{bmatrix}1&1\end{bmatrix}$ | -3 | |
| 8 | 0 | $\begin{bmatrix}1&1\end{bmatrix}$ | -3 | |
### 1.2.5 对偶形式
将 w 和 b 表示为实例$x_1$和标记$y_1$线性组合的形式,通过求解系数来求解w和b,前面提到过这个式子:
$w+\eta y_ix_i\to w$
$b+\eta y_i\to b$
这里先假设 w 和 b 的初值为0,那么通过对偶形式能表示为什么?从上面式子可以看出来,每次迭代,w会增加一个 $ηy_ix_i$,b 会增加一个$ηy_i$,到最后参数更新完之后,w 和 b 一共增加了这些:
$w=\sum_{i=1}^N\alpha_iy_ix_i$
$b=\sum_{i=1}^N\alpha_iy_i$
这里的$α_i = n_i*η$,$n_i$就是$(x_i,y_i)$被误分类的次数,η 还是学习率。
$\alpha_i$越大,意味这实例点更新次数越多,距离分离超平面越近,越难被分类,对实例影响结果越大
下面是对偶形式的参数更新过程:
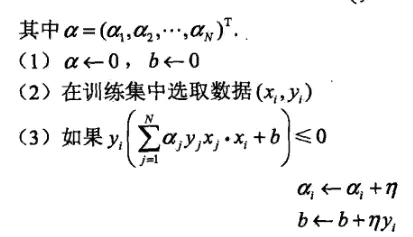
## 1.3 逻辑电路
### 1.3.1 与门
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
### 1.3.2 与非门
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
### 1.3.3 或门
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
### 1.3.4 异或门
什么是异或?就是,假如这里有两件事,一真一假,异或为真;两件事都为假或者两件事都为真,异或为假,就像这样:
0⊕0=0,0⊕1=1
1⊕0=1,1⊕1=0
下面是异或的函数图像:

通过图像可以看出,找不到一个超平面能将这四个点分隔开,所以**感知机无法处理异或问题,不仅仅是感知机,其他线性模型也无法处理这种问题。**
| $x_1$ | $x_2$ | y |
| ----- | ----- | ---- |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
#### 多层感知机mlp
如何解决呢???
使用多层的感知机即可完成,如下图所示

与门、与非门、或门的符号
通过上面的感知机如何组成异或门呢??

这里,把$s_1$作为 与非门 的输出,把$s_2$ 作为或门的输出,填入真值表中。
结果如图所示,观察$x_1、x_2 、y$,可以发现确实符合异或门的输出

异或门是一种多层结构的神经网络。
与门、或门是单层感知机,而异或门是2层感知机。叠加了多 层的感知机也称为多层感知机(multi-layered perceptron) 。

**感知机的作用就是引出神经网络**
# 2. 神经网络
参考资料
~~~bash
https://blog.csdn.net/as091313/article/details/79080583
~~~
## 2.1 概念
### 2.1.1 概念
人工神经网络(artificial neural network,ANN),简称神经网络(neural network,NN),是一种模仿生物神经网络的结构和功能的数学模型或计算模型。
神经网络是一种**运算模型**,由大量的节点(或称“神经元”)和之间相互的联接构成。
每个节点代表一种特定的输出函数,称为**激励函数、激活函数**(activation function)。
每两个节点间的联接都代表一个对于通过该连接信号的加权值,称之为权重,这相当于人工神经网络的记忆。
网络的输出则依网络的连接方式,权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近,也可能是对一种逻辑策略的表达。
### 2.1.2 应用-分类
神经网络最重要的用途是分类,为了让大家对分类有个直观的认识,咱们先看几个例子:
* 垃圾邮件识别:现在有一封电子邮件,把出现在里面的所有词汇提取出来,送进一个机器里,机器需要判断这封邮件是否是垃圾邮件。
* 疾病判断:病人到医院去做了一大堆肝功、尿检测验,把测验结果送进一个机器里,机器需要判断这个病人是否得病,得的什么病。
* 猫狗分类:有一大堆猫、狗照片,把每一张照片送进一个机器里,机器需要判断这幅照片里的东西是猫还是狗。
## 2.2 前期准备
资料参考
~~~bash
https://zhuanlan.zhihu.com/p/65472471
~~~
### 2.2.1 神经元
神经网络中最基本的成分是神经元模型,即上述定义中的简单单元

> $Inputs$:输入
>
> $Weights$:权值,权重
>
> $Bias$:偏置,或者称为阈值
>
> $Activationfunction$:激活函数
>
> 这种“阈值加权和”的神经元模型称为**M-P模型** ( McCulloch-Pitts Model ),也称为神经网络的**一个处理单元**( PE, Processing Element )。
### 2.2.2 激活函数
参考资料
~~~bash
https://zhuanlan.zhihu.com/p/25279356
~~~
> 激活函数是用来加入非线性因素的,解决线性模型所不能解决的问题。
>
> 简而言之,激活层是为矩阵运算的结果添加非线性的。
常用的激活函数有三种,分别是阶跃函数、Sigmoid和ReLU。不要被奇怪的函数名吓到,其实它们的形式都很简单,如下图(更正:sigmoid在负无穷是应趋近于0):

* 阶跃函数:当输入小于等于0时,输出0;当输入大于0时,输出1。
* Sigmoid:当输入趋近于正无穷/负无穷时,输出无限接近于1/0。
* ReLU:当输入小于0时,输出0;当输入大于0时,输出等于输入。
#### 1) sigmoid函数
sigmoid函数是一种常见的挤压函数,其将较大范围的输入挤压到$(0,1)$区间内,其函数的表达式与形状如下图所示:

该函数常被用于分类模型,因为其具有很好的一个特性$f^\prime(x)=f(x)(1-f(x))$.这个函数也会被用于下面的神经网络模型中做激活函数。
#### 2) 双极性Sigmoid函数
$$
h(x)=\frac{2}{1+e^{-\alpha x}}-1
\\ h^\prime(x)=\frac{2\alpha e^{-\alpha x}}{(1+e^{-\alpha x})}=\alpha\frac{1-h(x)^2}{2}
$$
例子
$f(x)-\frac{1-e^{-x}}{1+e^{-x}}$

#### 3) 阶跃函数
阶跃函数是一种特殊的连续时间函数,是一个从0跳变到1的过程,属于奇异函数

####
#### 4) ReLU
**线性整流函数**(Rectified Linear Unit, **ReLU**),又称**修正线性单元,**是一种人工神经网络中常用的激活函数(activation function)

### 2.2.3 层介绍
该模型与一个有向无环图相关联
$f(x)=f^{(3)}(f^{(2)}(f^{(1)}(x)))$
$f^{(1)}$被称为网络的第一层,叫做输入层
$f^{(2)}$被称为网络的第二层,叫做隐藏层
$f^{(3)}$被称为网络的第三层,叫做输出层

#### 1) 输入层
在我们的例子中,输入层是坐标值,例如$(1,1)$,这是一个包含两个元素的数组,也可以看作是一个$1\times 2$的矩阵。输入层的元素维度与输入量的特征息息相关,如果输入的是一张$32\times 32$像素的灰度图像,那么输入层的维度就是$32\times 32$。
#### 2) 隐藏层
连接输入层和隐藏层的是$W_1$和$b_1$。由X计算得到H十分简单,就是矩阵运算:
$$
H=X\cdot W_1+b_1
$$
如果你学过线性代数,对这个式子一定不陌生。如上图中所示,在设定隐藏层为50维(也可以理解成50个神经元)之后,矩阵H的大小为$1\times 50$的矩阵。
连接隐藏层和输出层的是W2和b2。同样是通过矩阵运算进行的:
$$
Y=H\cdot W_2+b_2
$$
**一系列线性方程的运算最终都可以用一个线性方程表示**
也就是说,上述两个式子联立后可以用一个线性方程表达。对于两次神经网络是这样,就算网络深度加到100层,也依然是这样。这样的话神经网络就失去了意义。
所以这里要对网络注入灵魂:**激活层**。
需要注意的是,每个隐藏层计算(矩阵线性运算)之后,都需要加一层激活层,要不然该层线性计算是没有意义的。

#### 3) 输出层
输出Y的值可能会是(3,1,0.1,0.5)这样的矩阵,诚然我们可以找到里边的最大值“3”,从而找到对应的分类为I,但是这并不直观。我们想让最终的输出为**概率**,也就是说可以生成像(90%,5%,2%,3%)这样的结果,这样做不仅可以找到最大概率的分类,而且可以知道各个分类计算的概率值。
具体是怎么计算的呢?
计算公式如下:
$S_i=\frac{e^i}{\sum_je^j}$
简单来说分三步进行:
(1)以e为底对所有元素求指数幂;
(2)将所有指数幂求和;
(3)分别将这些指数幂与该和做商。
这样求出的结果中,所有元素的和一定为1,而每个元素可以代表概率值。
我们将使用这个计算公式做输出结果正规化处理的层叫做“Softmax”层。此时的神经网络将变成

#### 4) Softmax-with-Loss 层
* Softmax层:将输入值正规化(输入值和调整为1,反映概率)后输出。
* Loss层:cross entropy error(交叉熵误差,一种损失函数)接收Softmax的输出(y1, y2, y3)和监督标签(t1, t2, t3), 输出损失L。

包含作为损失函数的交叉熵误差(cross entropy error),所以称为“Softmax-with-Loss层”。
Softmax-with-Loss层的计算图:

简易版Softmax-with-Loss层的计算图:

#### 5) Affine层
神经网络在传播时,进行的矩阵乘积运算。
神经网络的正向传播中,为了计算加权信号的总和,使用了矩阵的乘积运算(NumPy中是 np.dot())
神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”
如图:

## 2.3 损失函数
### 2.3.1 均方误差
$$
E=\frac{1}{2}\sum_{k}(y_k-t_k)^2
$$
$y_k$表示神经网络输出,$t_k$表示监督数据,k表示数据的维度
### 2.3.2 交叉熵误差
$$
E=-\sum_{k}t_klogy_k
$$
$y_k$表示神经网络输出,$t_k$表示监督数据,$k$表示数据的维度
$ log$是以e为底数的自然对数
参考文章
~~~bash
https://blog.csdn.net/qq_32790593/article/details/83619899
~~~
参考文章2
~~~bash
https://blog.csdn.net/qq_21966233/article/details/87189597
~~~