代码拉取完成，页面将自动刷新
The modified Version of this is in process: https://github.com/ArthasMenethil-A/Delta-Robot-Trajectory-Planning
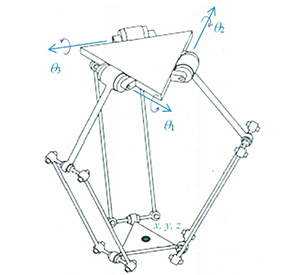
for the complete report on the theory of delta parallel robot please refer to my internship report this will be a step by step demonstration of how I experimented the different methods of trajectory planning for a Delta Parallel robot End-Effector
Overview:
with trajectory planning there are two fundemental questions we need an answer for:
The Delta robot is a 3-DOF robot that consists of two parallel platforms. One of them, which we call the EE platform, is capable of moving and the other one, which we call base platform, is not capable of that. These two platforms are connected with three arms. Each arm has one pin and two universal joints (as shown in the figure) that connect two solid rods. The rod which is connected to base platform by the pin, is called the active rod, and the other one is called the passive rod. The center of the base and EE platforms are marked as $O$ and $O'$ respectively. The pin is denoted as A, the universal joint connecting the passive and active rods, is denoted as B. The universal joint connecting the EE platform and the passive rod is denoted as C.
$\overrightarrow{(O O')} + \overrightarrow{(O' C_i)} = \overrightarrow{(O A_i)} + \overrightarrow{(A_i B_i)} + \overrightarrow{(B_i C_i)}$ (Equation 1)
here's a good playlist for learning FK and IK
you can see my python implementation of IK:
this section is dedicated to answer how should you go about writing a code for point to point movement (moving the EE from point 1 to point 2 in 3d space )
In order to represent each joint motion, a fifth-order polynomial $s(\tau)$ is used here. meaning that, if $\theta_0$ and $\theta_1$ and the corresponding time instants of $t_0$ and $t_1$ are given, the path between them can be interpolated by use of a fifth order polynomial that outputs a predicted $\theta_{pred}(t)$ that $t \ \in \ [t_0, \ t_1]$
the polynomial is shown in the following form \[s(\tau) = a\tau^5 + b\tau^4 + c\tau^3 + d\tau^2 + e\tau + f\] such that \[0 \leq s \leq 1 \quad 0 \leq \tau \leq 1\] and \[\tau = \frac{t}{T}\] we will thus aim at a normal polynomial that, upon scaling both its argument and the polynomial itself, will allow us to represent each of the joint variables $\theta_j$ throughout its range of motion so that: \[\theta(t) = \theta_I + (\theta_F - \theta_I)s(\tau)\] and $\frac{d \theta}{dt}, \ \frac{d^2 \theta}{d t^2}, \ \frac{d^3 \theta}{d t^3}$ are calculated by defferentiating the above formula with the boundary conditions at \[s(0), \ s^\prime (0), \ s^{\prime \prime} (0), \ s(1), \ s^\prime (1), \ s^{\prime \prime} (0)\]
The problem with 3-4-5 polynomial is that the jerk at the boundary can't be set to zero, for this problem we use a higher degree of polynomial, namely, 7-th deg polynomial.
with the steps similar to the last section and the added boundary conditions of $s^{\prime \prime \prime}(0), \ s^{\prime \prime \prime}(1)$ we solve the system of question generated from the boudary conditions.
3-4-5 polynomial and 4-5-6-7 polynomial point to point movement, you can learn about this in the book "Fundamentals of Robotic Mechanical Systems, theory, methods, and Algorithms, Fourth Edition by Jorge Angeles - chapter 6"
In Trapezoidal method we have 3 phases,
$V = a.t \quad for \quad 0 \leq t \leq T_a$
$V = V_{max} \quad for \quad T_a \leq t \leq T - T_a$
$V = -a.t \quad for \quad T-T_a \leq t \leq T$
you can find the codes related to trapezoidal point to poitn movement in this source code
This is the resultant plot:
as a concept, s-curve is the better version of trapezoidal. strictly speaking, it has seven phases instead of three. as explained blow in mathemathis terms:
$a = J.t \quad for \quad T_0 \leq t \leq T_1$
$a = a_{max} \quad for \quad T_1 \leq t \leq T_2$
$a = J(T_3 - t) \quad for \quad T_2 \leq t \leq T_3$
$a = 0 \quad for \quad T_3 \leq t \leq T_4$
$a = -J(t - T_4) \quad for \quad T_4 \leq t \leq T_5$
$a = -a_{max} \quad for \quad T_5 \leq t \leq T_6$
$a = -J(T_7 - t) \quad for \quad T_6 \leq t \leq T_7$
this section is dedicated to planning out a specific trajectory for the robot to go through
one way of interpolating a path of $n+1$ points in space, is by a polynomial of degree $n$. This way might work for 3 or 4 points, but fir higer degree polynomials it can be very computationally expensive. Another way which is much better in terms of computational power needed, is using $n$ polynomials of degree $p$ that $p << n$. The overall function $s(t)$ defined in this manner is called a spline of degree $p$.
Computation of the coefficient for assigned initial and final velocities plot:
Computation of the coefficient for assigned initial and final velocities and acceleration plot:
cubic spline (book Trajectory Planning for Automatix Machines and Robots by Luigi Biagiotti and Claudio Melchiorri)
a very common method to obtain trajectoryies with a continuous velocity profile is to use linear motions with parabolic blends, characterized therefore by the typical trapezoidal velocity profiles.
To achieve something like this first we need to initiate a form of velocity prfile and then modify it
If the method from point to point trapezoidal movement is used directly for multi-point, velocity becomes zero quite often and in every pre-defined point in the path, which is not acceptable. this kind of behaviour can be seen in the plot below:
\textbf{Theory and algorithm of modifying the velocity profile above}
after modifying this velocity profile we get the following plots:
The jacobian matrix relates velocity of EE to the velocity of actuator joints with the relation: $\vec{v} = J \dot{\vec{\theta}}$
for the IK we have the equations as followed
from these equation we solve for $\theta_{ij}$ (solution of IK) and solve for $p_x, p_y, p_z$ (solution of FK)
further explanation in the following pdf that i've written according the mentioned references: jacobian, IK and FK
此处可能存在不合适展示的内容，页面不予展示。您可通过相关编辑功能自查并修改。
如您确认内容无涉及 不当用语 / 纯广告导流 / 暴力 / 低俗色情 / 侵权 / 盗版 / 虚假 / 无价值内容或违法国家有关法律法规的内容，可点击提交进行申诉，我们将尽快为您处理。
马建仓 AI 助手